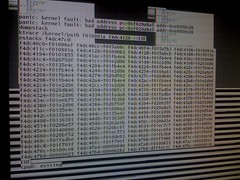
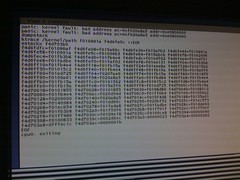
Note: This is an experimental planet, if you have a feed you would like to add or you would like your feed to be removed please contact me.
Planet 9
October 11, 2012
October 07, 2012
NineTimes - Inferno and Plan 9 News
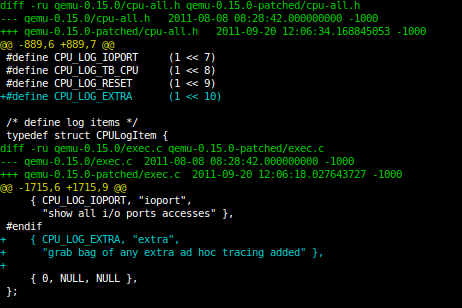
9FRONT "MOTHY MARTHA" Released
New 9front release "MOTHY MARTHA"
the changes from previous release include:
mothra improvements: fast scroll, text selection
updated manual pages
hjfs improvments and bugfixes
added "Rules of Acquisition" (/lib/roa)
devproc bugfixes
improved guesscpuhz()
fixed tftp lost ack packet bug
added eriks atazz and disk/smart
sata support for 4K sector drives

October 04, 2012
September 23, 2012
Command Center

Thank you Apple
Some days, things just don't work out. Or don't work.
Earlier
I wanted to upgrade (their term, not mine) my iMac from Snow Leopard (10.6) to Lion (10.7). I even had the little USB stick version of the installer, to make it easy. But after spending some time attempting the installation, the Lion installer "app" failed, complaining about SMART errors on the disk.Disk Utility indeed reported there were SMART errors, and that the disk hardware needed to be replaced. An ugly start.
The good news is that in some places, including where I live, Apple will do a house call for service, so I didn't have to haul the computer to an Apple store on public transit.
Thank you Apple.
I called them, scheduled the service for a few days later, and as instructed by Apple (I hardly needed prompting) prepped a backup using Time Machine.
The day before the repairman was to come to give me a new disk, I made sure the system was fully backed up, for security reasons started a complete erasure of the bad disk (using Disk Utility in target mode from another machine, about which more later), and went to bed.
The day
When I got up, I checked that the disk had been erased and headed off to work. As I left the apartment, the ceiling lights in the entryway flickered and then went out: a new bulb was needed. On the way out of the building, I asked the doorman for a replacement bulb. He offered just to replace it for us. We have a good doorman.Once at work, things were normal until my cell phone rang about 2pm. It was the Apple repairman, Twinkletoes (some names and details have been changed), calling to tell me he'd be at my place within the hour. Actually, he wasn't an Apple employee, but a contractor working for Unisys, a name I hadn't heard in a long time. (Twinkletoes was a name I hadn't heard for a while either, but that's another story.) At least here, Apple uses Unisys contractors to do their house calls.
So I headed home, arriving before Twinkletoes. At the front door, the doorman stopped me. He reported that the problem with the lights was not the bulb, but the wiring. He'd called in an electrician, who had found a problem in the breaker box and fixed it. Everything was good now.
When I got up to the apartment, I found chaos: the cleaners were mid-job, with carpets rolled up, vacuum cleaners running, and general craziness. Not conducive to work. So I went back down to the lobby with my laptop and sat on the couch, surfing on the free WiFi from the café next door, and waited for Twinkletoes.
Half an hour later, he arrived and we returned to the apartment. The cleaners were still there but the chaos level had dropped and it wasn't too hard to work around them. I saw what the inside of an iMac looks like as Twinkletoes swapped out the drive. By the time he was done, the cleaners had left and things had settled down.
I had assumed that the replacement drive would come with an installed operating system, but I assumed wrong. (When you assume, you put plum paste on your ass.) I had a Snow Leopard installation DVD, but I was worried: it had failed to work for me a few days earlier when I wanted to boot from it to run fsck on the broken drive. Twinkletoes noticed it had a scratch. I needed another way to boot the machine.
It had surprised me when Lion came out that the installation was done by an "app", not as a bootable image. This is an unnecessary complication for those of us that need to maintain machines. Earlier, when updating a different machine, I had learned how painful this could be when the installation app destroyed the boot sector and I needed to reinstall Snow Leopard from DVD, and then upgrade that to a version of the system recent enough to run the Lion installer app. As will become apparent, had Lion come as a bootable image things might have gone more smoothly.
Thank you Apple.
[Note added in post: Several people have told me there's a bootable image inside the installer. I forgot to mention that I knew that, and there wasn't. For some reason, the version on the USB stick I have looks different from the downloaded one I checked out a day or two later, and even Twinkletoes couldn't figure out how to unpack it. Weird.]
Twinkletoes had an OS image he was willing to let me copy, but I needed to make a bootable drive from it. I had no sufficiently large USB stick—you need a 4GB one you can wipe. However I did have a free, big enough CompactFlash card and a USB reader, so that should do, right? Twinkletoes was unsure but believed it would.
Using my laptop, I used Disk Utility to create a bootable image on the CF card from Twinkletoes's disk image. We were ready.
Plug in the machine, push down the Option key, power on.
Nothing.
Turn on the light.
Nothing.
No power.
The cleaners must have tripped a breaker.
I went to the breaker box and found that all the breakers looked OK. We now had a mystery, because the cleaners had had lights on and were using electric appliances—I saw a vacuum cleaner running—but now there was no power. Was the power off to the building? No: the lights still worked in the kitchen and the oven clock was lit. I called the doorman and asked him to get the electrician back as soon as possible and then, with a little portable lamp, went looking around the apartment for a working socket. I found one, again in the kitchen. The iMac was going to travel after all, if not as far as downtown.
The machine was moved, plugged in, option-key-downed, and powered on. I selected the CF card to boot from, waited 15 minutes for the installation to come up, only to have the boot fail. CF cards don't work after all, although the diagnosis of failure is a bit tardy and uninformative.
Thank you Apple.
Next idea. My old laptop has FireWire so we could bring the disk up using target mode and then run the installer on the laptop to install Lion on the iMac.
We did the target mode dance and connected to the newly installed drive, then ran Disk Utility on the laptop to format the drive. Things were starting to look better.
Next, we put the Lion installer stick into the laptop, which was running a recent version of Snow Leopard.
Failure again. This time the problem is that the laptop, all of about four years old, is too old to run Lion. It's got a Core Duo, not a Core 2 Duo, and Lion won't run on that hardware. Even though Lion doesn't need to run, only the Lion installer needs to run, the system refuses to help. My other laptop is new enough to run the installer, but it doesn't have FireWire so it can't do target mode.
Thank you Apple. Your aggressive push to retire old technology hurts sometimes, you know? Actually, more than sometimes, but let's stay on topic.
Twinkletoes has to leave—he's been on the job for several hours now—but graciously lends me a USB boot drive he has, asking me to return it by post when I'm done. I thank him profusely and send him away before he is drawn in any deeper.
Using his boot drive, I was able to bring up the iMac and use the Lion installer stick to get the system to a clean install state. Finally, a computer, although of course all my personal data is over on the backup.
When a new OS X installation comes up, it presents the option of "migrating" data from an existing system, including from a Time Machine backup. So I went for that option and connected the external drive with the Time Machine backup on it.
The Migration Assistant presented a list of disks to migrate from. A list of one: the main drive in the machine. It didn't give me the option of using the Time Machine backup.
Thank you Apple. You told me to save my machine this way but then I can't use this backup to recover.
I called Apple on my cell phone (there's still no power in the room with the land line's wireless base station) and explained the situation. The sympathetic but ultimately unhelpful person on the phone said it should work (of course!) and that I should run Software Update and get everything up to the latest version. He reported that there were problems with the Migration Assistant in early versions of the Lion OS, and my copy of the installer was pretty early.
I started the upgrade process, which would take a couple of hours, and took my laptop back down to the lobby for some free WiFi to kill time. But it's now evening, the café is closed, and there is no WiFi. Naturally.
Back to the apartment, grab a book, return to the lobby to wait for the electrician.
An hour or so later, the electrician arrived and we returned to the apartment to see what was wrong. It was easy to diagnose. He had made a mistake in the fix, in fact a mistake related to what was causing the original problem. The breaker box has a silly design that makes it too easy to break a connection when working in the box, and that's what had happened. So it was easy to fix and easy to verify that it was fixed, but also easy to understand why it had happened. No excuses, but problem solved and power was now restored.
The computer was still upgrading but nearly done, so a few minutes later I got to try migrating again. Same result, naturally, and another call to Apple and this time little more than an apology. The unsatisfactory solution: do a clean installation and manually restore what's important from the Time Machine backup.
Thank you Apple.
It was fairly straightforward, if slow, to restore my personal files from the home directory on the backup, but the situation for installed software was dire. Restoring an installed program, either using the ludicrous Time Machine UI or copying the files by hand, is insufficient in most cases to bring back the program because you also need manifests and keys and receipts and whatnot. As a result, things such as iWork (Keynote etc.) and Aperture wouldn't run. I could copy every piece of data I could find but the apps refused to let me run them. Despite many attempts digging far too deep into the system, I could not get the right pieces back from the Time Machine backup. Worse, the failure modes were appalling: crashes, strange display states, inexplicable non-workiness. A frustating mess, but structured perfectly to belong on this day.
For peculiar reasons I didn't have the installation disks for everything handy, so these (expensive!) programs were just gone, even though I had backed up everything as instructed.
Thank you Apple.
I did have some installation disks, so for instance I was able to restore Lightroom and Photoshop, but then of course I needed to wait for huge updates to download even though the data needed was already sitting on the backup drive.
Back on the phone for the other stuff. Because I could prove that I had paid for the software, Apple agreed to send me fresh installation disks for everything of theirs but Aperture, but that would take time. In fact, it took almost a month for the iWork DVD to arrive, which is unacceptably long. I even needed to call twice to remind them before the disks were shipped.
The Aperture story was more complicated. After a marathon debugging session I managed to get it to start but then it needed the install key to let me do anything. I didn't have the disk, so I didn't know the key. Now, Aperture is from part of the company called Pro Tools or something like that, and they have a different way of working. I needed to contact them separately to get Aperture back. It's important to understand I hadn't lost my digital images. They were backed up multiple times, including in the network, on the Time Machine backup, and also on an external drive using the separate "vault" mechanism that is one of the best features of Aperture.
I reached the Aperture people on the phone and after a condensed version of the story convinced them I needed an install key (serial number) to run the version of Aperture I'd copied from the Time Machine backup. I was berated by the person on the phone: Time Machine is not suitable for backing up Aperture databases. (What? Your own company's backup solution doesn't know how to back up? Thank you Apple.) After a couple more rounds of abuse, I convinced the person on the phone that a) I was backing up my database as I should, using an Aperture vault and b) it wasn't the database that was the problem, but the program. I was again told that wasn't a suitable way to back up (again, What?), at which point I surrendered and just begged for an installation key, which was provided, and I could again run Aperture. This was the only time in the story where the people I was interacting with were not at least sympathetic to my situation. I guess Pro is a synonym for unfriendly.
Thank you Apple.
There's much more to the story. It took weeks to get everything working again properly. The complete failure of Time Machine to back up my computer's state properly was shocking to me. After this fiasco, I learned about the Lion Recovery App, which everyone who uses Macs should know about, but was not introduced until well after Lion rolled out with its preposterous not-bootable installation setup. The amount of data I already had on my backup disk but that needed to be copied from the net again was laughable. And there were total mysteries, like GMail hanging forever for the first day or so, a problem that may be unrelated or may just be the way life was this day.
But, well after midnight, worn out, beat up, tired, but with electricity restored and a machine that had a little life in it again, I powered down, took the machine back to my office and started to get ready for bed. Rest was needed and I had had enough of technology for one day.
One more thing
Oh yes, one more thing. There's always one more thing in our technological world.I walked into the bathroom for my evening ablutions only to have the toilet seat come off completely in my hand.
Just because you started it all, even for this,
Thank you Apple.
September 22, 2012
September 18, 2012
NineTimes - Inferno and Plan 9 News
9FRONT "OFF KEY LEE" Released
New 9front release "OFF KEY LEE"
changes include:
ACPI improvement (AliasOp AML instruction)
USB unassigned PciINTL work arround
Intel SCH busmastering dma support
mothra improvements (<script> tag, line break layout bugfix)
HTML support for lp
rio one line increment scroll (Shift)

September 17, 2012
research!rsc

A Tour of Acme
People I work with recognize my computer easily: it's the one with nothing but yellow windows and blue bars on the screen. That's the text editor acme, written by Rob Pike for Plan 9 in the early 1990s. Acme focuses entirely on the idea of text as user interface. It's difficult to explain acme without seeing it, though, so I've put together a screencast explaining the basics of acme and showing a brief programming session. Remember as you watch the video that the 854x480 screen is quite cramped. Usually you'd run acme on a larger screen: even my MacBook Air has almost four times as much screen real estate.
The video doesn't show everything acme can do, nor does it show all the ways you can use it. Even small idioms like where you type text to be loaded or executed vary from user to user. To learn more about acme, read Rob Pike's paper “Acme: A User Interface for Programmers” and then try it.
Acme runs on most operating systems. If you use Plan 9 from Bell Labs, you already have it. If you use FreeBSD, Linux, OS X, or most other Unix clones, you can get it as part of Plan 9 from User Space. If you use Windows, I suggest trying acme as packaged in acme stand alone complex, which is based on the Inferno programming environment.
Mini-FAQ:
- Q. Can I use scalable fonts? A. On the Mac, yes. If you run
acme -f /mnt/font/Monaco/16a/fontyou get 16-point anti-aliased Monaco as your font, served via fontsrv. If you'd like to add X11 support to fontsrv, I'd be happy to apply the patch. - Q. Do I need X11 to build on the Mac? A. No. The build will complain that it cannot build ‘snarfer’ but it should complete otherwise. You probably don't need snarfer.
If you're interested in history, the predecessor to acme was called help. Rob Pike's paper “A Minimalist Global User Interface” describes it. See also “The Text Editor sam”
Correction: the smiley program in the video was written by Ken Thompson. I got it from Dennis Ritchie, the more meticulous archivist of the pair.
September 07, 2012
September 06, 2012
NineTimes - Inferno and Plan 9 News
9FRONT "ROBBY RUBBISH" Released
New 9front "Robby Rubbish"
Changes include support for Intel 82567V ethernet and USB fixes for isochronous transfers (usb audio) and support for SK-8835 IBM Thinkpad USB Keyboard/Mice. date(1) got support to print ISO-8601 date and time and devshr now honors the noattach flag (RFNOMNT).

August 30, 2012
NineTimes - Inferno and Plan 9 News
9FRONT "RELEASE TARGET GERONIMO" Released
New 9front "Release Target Geronimo"
changes include:
aux/cpuid program to print Intel cpu features
netaudit program which checks network database for common mistakes
bugfixes for ndb/dns
fixed old RFNOMNT kernel bug
fix sleep / wakeup bug in devmnt and sdvirtio
pause function in games/gb
rio listing burried windows in button 3 menu
audiohda support for Intel SCH Pouslbo and Oaktrail
usb/kb support for Microsoft Sidewinder X5 Mouse
default configuration for 9bootpxe
tls support for sha256WithRSAEncryption (torproject.com)
bugfixes in jpg

August 12, 2012
NineTimes - Inferno and Plan 9 News
9FRONT "GROOGY GREG" Released
New 9front release "Groovy Greg"
changes include:
- new experimental hjfs filesystem (also avialable as install option)
- native graphics support fixed for vmware and qemu
- ps -n option to print note group
- ppp noauth option
- various bug fixes (icmp frag handling, pci *nobios, audioac97, floppy driver, zipfs, eenter())

August 03, 2012
August 01, 2012
NineTimes - Inferno and Plan 9 News
9FRONT "DEAF GEOFF" Released
New 9front release "Deaf Geoff"
this release consists mainly of bugfixes (cwfs, kfs, factotum, mothra) tho cdfs got updated from sources and sam undo command will jump to the change now (thanks aiju!) ;)

July 04, 2012
Command Center

Less is exponentially more
Here is the text of the talk I gave at the Go SF meeting in June, 2012.
This is a personal talk. I do not speak for anyone else on the Go team here, although I want to acknowledge right up front that the team is what made and continues to make Go happen. I'd also like to thank the Go SF organizers for giving me the opportunity to talk to you.
I was asked a few weeks ago, "What was the biggest surprise you encountered rolling out Go?" I knew the answer instantly: Although we expected C++ programmers to see Go as an alternative, instead most Go programmers come from languages like Python and Ruby. Very few come from C++.
We—Ken, Robert and myself—were C++ programmers when we designed a new language to solve the problems that we thought needed to be solved for the kind of software we wrote. It seems almost paradoxical that other C++ programmers don't seem to care.
I'd like to talk today about what prompted us to create Go, and why the result should not have surprised us like this. I promise this will be more about Go than about C++, and that if you don't know C++ you'll be able to follow along.
The answer can be summarized like this: Do you think less is more, or less is less?
Here is a metaphor, in the form of a true story. Bell Labs centers were originally assigned three-letter numbers: 111 for Physics Research, 127 for Computing Sciences Research, and so on. In the early 1980s a memo came around announcing that as our understanding of research had grown, it had become necessary to add another digit so we could better characterize our work. So our center became 1127. Ron Hardin joked, half-seriously, that if we really understood our world better, we could drop a digit and go down from 127 to just 27. Of course management didn't get the joke, nor were they expected to, but I think there's wisdom in it. Less can be more. The better you understand, the pithier you can be.
Keep that idea in mind.
Back around September 2007, I was doing some minor but central work on an enormous Google C++ program, one you've all interacted with, and my compilations were taking about 45 minutes on our huge distributed compile cluster. An announcement came around that there was going to be a talk presented by a couple of Google employees serving on the C++ standards committee. They were going to tell us what was coming in C++0x, as it was called at the time. (It's now known as C++11).
In the span of an hour at that talk we heard about something like 35 new features that were being planned. In fact there were many more, but only 35 were described in the talk. Some of the features were minor, of course, but the ones in the talk were at least significant enough to call out. Some were very subtle and hard to understand, like rvalue references, while others are especially C++-like, such as variadic templates, and some others are just crazy, like user-defined literals.
At this point I asked myself a question: Did the C++ committee really believe that was wrong with C++ was that it didn't have enough features? Surely, in a variant of Ron Hardin's joke, it would be a greater achievement to simplify the language rather than to add to it. Of course, that's ridiculous, but keep the idea in mind.
Just a few months before that C++ talk I had given a talk myself, which you can see on YouTube, about a toy concurrent language I had built way back in the 1980s. That language was called Newsqueak and of course it is a precursor to Go.
I gave that talk because there were ideas in Newsqueak that I missed in my work at Google and I had been thinking about them again. I was convinced they would make it easier to write server code and Google could really benefit from that.
I actually tried and failed to find a way to bring the ideas to C++. It was too difficult to couple the concurrent operations with C++'s control structures, and in turn that made it too hard to see the real advantages. Plus C++ just made it all seem too cumbersome, although I admit I was never truly facile in the language. So I abandoned the idea.
But the C++0x talk got me thinking again. One thing that really bothered me—and I think Ken and Robert as well—was the new C++ memory model with atomic types. It just felt wrong to put such a microscopically-defined set of details into an already over-burdened type system. It also seemed short-sighted, since it's likely that hardware will change significantly in the next decade and it would be unwise to couple the language too tightly to today's hardware.
We returned to our offices after the talk. I started another compilation, turned my chair around to face Robert, and started asking pointed questions. Before the compilation was done, we'd roped Ken in and had decided to do something. We did not want to be writing in C++ forever, and we—me especially—wanted to have concurrency at my fingertips when writing Google code. We also wanted to address the problem of "programming in the large" head on, about which more later.
We wrote on the white board a bunch of stuff that we wanted, desiderata if you will. We thought big, ignoring detailed syntax and semantics and focusing on the big picture.
I still have a fascinating mail thread from that week. Here are a couple of excerpts:
Robert: Starting point: C, fix some obvious flaws, remove crud, add a few missing features.
Rob: name: 'go'. you can invent reasons for this name but it has nice properties. it's short, easy to type. tools: goc, gol, goa. if there's an interactive debugger/interpreter it could just be called 'go'. the suffix is .go.
Robert Empty interfaces: interface {}. These are implemented by all interfaces, and thus this could take the place of void*.
We didn't figure it all out right away. For instance, it took us over a year to figure out arrays and slices. But a significant amount of the flavor of the language emerged in that first couple of days.
Notice that Robert said C was the starting point, not C++. I'm not certain but I believe he meant C proper, especially because Ken was there. But it's also true that, in the end, we didn't really start from C. We built from scratch, borrowing only minor things like operators and brace brackets and a few common keywords. (And of course we also borrowed ideas from other languages we knew.) In any case, I see now that we reacted to C++ by going back down to basics, breaking it all down and starting over. We weren't trying to design a better C++, or even a better C. It was to be a better language overall for the kind of software we cared about.
In the end of course it came out quite different from either C or C++. More different even than many realize. I made a list of significant simplifications in Go over C and C++:
- regular syntax (don't need a symbol table to parse)
- garbage collection (only)
- no header files
- explicit dependencies
- no circular dependencies
- constants are just numbers
- int and int32 are distinct types
- letter case sets visibility
- methods for any type (no classes)
- no subtype inheritance (no subclasses)
- package-level initialization and well-defined order of initialization
- files compiled together in a package
- package-level globals presented in any order
- no arithmetic conversions (constants help)
- interfaces are implicit (no "implements" declaration)
- embedding (no promotion to superclass)
- methods are declared as functions (no special location)
- methods are just functions
- interfaces are just methods (no data)
- methods match by name only (not by type)
- no constructors or destructors
- postincrement and postdecrement are statements, not expressions
- no preincrement or predecrement
- assignment is not an expression
- evaluation order defined in assignment, function call (no "sequence point")
- no pointer arithmetic
- memory is always zeroed
- legal to take address of local variable
- no "this" in methods
- segmented stacks
- no const or other type annotations
- no templates
- no exceptions
- builtin string, slice, map
- array bounds checking
And yet, with that long list of simplifications and missing pieces, Go is, I believe, more expressive than C or C++. Less can be more.
But you can't take out everything. You need building blocks such as an idea about how types behave, and syntax that works well in practice, and some ineffable thing that makes libraries interoperate well.
We also added some things that were not in C or C++, like slices and maps, composite literals, expressions at the top level of the file (which is a huge thing that mostly goes unremarked), reflection, garbage collection, and so on. Concurrency, too, naturally.
One thing that is conspicuously absent is of course a type hierarchy. Allow me to be rude about that for a minute.
Early in the rollout of Go I was told by someone that he could not imagine working in a language without generic types. As I have reported elsewhere, I found that an odd remark.
To be fair he was probably saying in his own way that he really liked what the STL does for him in C++. For the purpose of argument, though, let's take his claim at face value.
What it says is that he finds writing containers like lists of ints and maps of strings an unbearable burden. I find that an odd claim. I spend very little of my programming time struggling with those issues, even in languages without generic types.
But more important, what it says is that types are the way to lift that burden. Types. Not polymorphic functions or language primitives or helpers of other kinds, but types.
That's the detail that sticks with me.
Programmers who come to Go from C++ and Java miss the idea of programming with types, particularly inheritance and subclassing and all that. Perhaps I'm a philistine about types but I've never found that model particularly expressive.
My late friend Alain Fournier once told me that he considered the lowest form of academic work to be taxonomy. And you know what? Type hierarchies are just taxonomy. You need to decide what piece goes in what box, every type's parent, whether A inherits from B or B from A. Is a sortable array an array that sorts or a sorter represented by an array? If you believe that types address all design issues you must make that decision.
I believe that's a preposterous way to think about programming. What matters isn't the ancestor relations between things but what they can do for you.
That, of course, is where interfaces come into Go. But they're part of a bigger picture, the true Go philosophy.
If C++ and Java are about type hierarchies and the taxonomy of types, Go is about composition.
Doug McIlroy, the eventual inventor of Unix pipes, wrote in 1964 (!):
We should have some ways of coupling programs like garden hose--screw in another segment when it becomes necessary to massage data in another way. This is the way of IO also.That is the way of Go also. Go takes that idea and pushes it very far. It is a language of composition and coupling.
The obvious example is the way interfaces give us the composition of components. It doesn't matter what that thing is, if it implements method M I can just drop it in here.
Another important example is how concurrency gives us the composition of independently executing computations.
And there's even an unusual (and very simple) form of type composition: embedding.
These compositional techniques are what give Go its flavor, which is profoundly different from the flavor of C++ or Java programs.
===========
There's an unrelated aspect of Go's design I'd like to touch upon: Go was designed to help write big programs, written and maintained by big teams.
There's this idea about "programming in the large" and somehow C++ and Java own that domain. I believe that's just a historical accident, or perhaps an industrial accident. But the widely held belief is that it has something to do with object-oriented design.
I don't buy that at all. Big software needs methodology to be sure, but not nearly as much as it needs strong dependency management and clean interface abstraction and superb documentation tools, none of which is served well by C++ (although Java does noticeably better).
We don't know yet, because not enough software has been written in Go, but I'm confident Go will turn out to be a superb language for programming in the large. Time will tell.
===========
Now, to come back to the surprising question that opened my talk:
Why does Go, a language designed from the ground up for what what C++ is used for, not attract more C++ programmers?
Jokes aside, I think it's because Go and C++ are profoundly different philosophically.
C++ is about having it all there at your fingertips. I found this quote on a C++11 FAQ:
The range of abstractions that C++ can express elegantly, flexibly, and at zero costs compared to hand-crafted specialized code has greatly increased.That way of thinking just isn't the way Go operates. Zero cost isn't a goal, at least not zero CPU cost. Go's claim is that minimizing programmer effort is a more important consideration.
Go isn't all-encompassing. You don't get everything built in. You don't have precise control of every nuance of execution. For instance, you don't have RAII. Instead you get a garbage collector. You don't even get a memory-freeing function.
What you're given is a set of powerful but easy to understand, easy to use building blocks from which you can assemble—compose—a solution to your problem. It might not end up quite as fast or as sophisticated or as ideologically motivated as the solution you'd write in some of those other languages, but it'll almost certainly be easier to write, easier to read, easier to understand, easier to maintain, and maybe safer.
To put it another way, oversimplifying of course:
Python and Ruby programmers come to Go because they don't have to surrender much expressiveness, but gain performance and get to play with concurrency.
C++ programmers don't come to Go because they have fought hard to gain exquisite control of their programming domain, and don't want to surrender any of it. To them, software isn't just about getting the job done, it's about doing it a certain way.
The issue, then, is that Go's success would contradict their world view.
And we should have realized that from the beginning. People who are excited about C++11's new features are not going to care about a language that has so much less. Even if, in the end, it offers so much more.
Thank you.
June 24, 2012
June 21, 2012
research!rsc

A Tour of Go
Last week, I gave a talk about Go at the Boston Google Developers Group meeting. There were some problems with the recording, so I have rerecorded the talk as a screencast and posted it on YouTube.
Here are the answers to questions asked at the end of the talk.
Q. How does Go work with debuggers?
To start, both Go toolchains include debugging information that gdb can read in the final binaries, so basic gdb functionality works on Go programs just as it does on C programs.
We’ve talked for a while about a custom Go debugger, but there isn’t one yet.
Many of the programs we want to debug are live, running programs. The net/http/pprof package provides debugging information like goroutine stacks, memory profiling, and cpu profiling in response to special HTTP requests.
Q. If a goroutine is stuck reading from a channel with no other references, does the goroutine get garbage collected?
No. From the garbage collection point of view, both sides of the channel are represented by the same pointer, so it can’t distinguish the receive and send sides. Even if we could detect this situation, we’ve found that it’s very useful to keep these goroutines around, because the program is probably heading for a deadlock. When a Go program deadlocks, it prints all its goroutine stacks and then exits. If we garbage collected the goroutines as they got stuck, the deadlock handler wouldn’t have anything useful to print except "your entire program has been garbage collected".
Q. Can a C++ program call into Go?
We wrote a tool called cgo so that Go programs can call into C, and we’ve implemented support for Go in SWIG, so that Go programs can call into C++. In those programs, the C or C++ can in turn call back into Go. But we don’t have support for a C or C++ program—one that starts execution in the C or C++ world instead of the Go world—to call into Go.
The hardest part of the cross-language calls is converting between the C calling convention and the Go calling convention, specifically with the regard to the implementation of segmented stacks. But that’s been done and works.
Making the assumption that these mixed-language binaries start in Go has simplified a number of parts of the implementation. I don’t anticipate any technical surprises involved in removing these assumptions. It’s just work.
Q. What are the areas that you specifically are trying to improve the language?
For the most part, I’m not trying to improve the language itself. Part of the effort in preparing Go 1 was to identify what we wanted to improve and do it. Many of the big changes were based on two or three years of experience writing Go programs, and they were changes we’d been putting off because we knew that they’d be disruptive. But now that Go 1 is out, we want to stop changing things and spend another few years using the language as it exists today. At this point we don’t have enough experience with Go 1 to know what really needs improvement.
My Go work is a small amount of fixing bugs in the libraries or in the compiler and a little bit more work trying to improve the performance of what’s already there.
Q. What about talking to databases and web services?
For databases, one of the packages we added in Go 1 is a standard database/sql package. That package defines a standard API for interacting with SQL databases, and then people can implement drivers that connect the API to specific database implementations like SQLite or MySQL or Postgres.
For web services, you’ve seen the support for JSON and XML encodings. Those are typically good enough for ad hoc REST services. I recently wrote a package for connecting to the SmugMug photo hosting API, and there’s one generic call that unmarshals the response into a struct of the appropriate type, using json.Unmarshal. I expect that XML-based web services like SOAP could be framed this way too, but I’m not aware of anyone who’s done that.
Inside Google, of course, we have plenty of services, but they’re based on protocol buffers, so of course there’s a good protocol buffer library for Go.
Q. What about generics? How far off are they?
People have asked us about generics from day 1. The answer has always been, and still is, that it’s something we’ve put a lot of thought into, but we haven’t yet found an approach that we think is a good fit for Go. We’ve talked to people who have been involved in the design of generics in other languages, and they’ve almost universally cautioned us not to rush into something unless we understand it very well and are comfortable with the implications. We don’t want to do something that we’ll be stuck with forever and regret.
Also, speaking for myself, I don’t miss generics when I write Go programs. What’s there, having built-in support for arrays, slices, and maps, seems to work very well.
Finally, we just made this promise about backwards compatibility with the release of Go 1. If we did add some form of generics, my guess is that some of the existing APIs would need to change, which can’t happen until Go 2, which I think is probably years away.
Q. What types of projects does Google use Go for?
Most of the things we use Go for I can’t talk about. One notable exception is that Go is an App Engine language, which we announced at I/O last year. Another is vtocc, a MySQL load balancer used to manage database lookups in YouTube’s core infrastructure.
Q. How does the Plan 9 toolchain differ from other compilers?
It’s a completely incompatible toolchain in every way. The main difference is that object files don’t contain machine code in the sense of having the actual instruction bytes that will be used in the final binary. Instead they contain a custom encoding of the assembly listings, and the linker is in charge of turning those into actual machine instructions. This means that the assembler, C compiler, and Go compiler don’t all duplicate this logic. The main change for Go is the support for segmented stacks.
I should add that we love the fact that we have two completely different compilers, because it keeps us honest about really implementing the spec.
Q. What are segmented stacks?
One of the problems in threaded C programs is deciding how big a stack each thread should have. If the stack is too small, then the thread might run out of stack and cause a crash or silent memory corruption, and if the stack is too big, then you’re wasting memory. In Go, each goroutine starts with a small stack, typically 4 kB, and then each function checks if it is about to run out of stack and if so allocates a new stack segment that gets recycled once it’s not needed anymore.
Gccgo supports segmented stacks, but it requires support added recently to the new GNU linker, gold, and that support is only implemented for x86-32 and x86-64.
Segmented stacks are something that lots of people have done before in experimental or research systems, but they have never made it into the C toolchains.
Q. What is the overhead of segmented stacks?
It’s a few instructions per function call. It’s been a long time since I tried to measure the precise overhead, but in most programs I expect it to be not more than 1-2%. There are definitely things we could do to try to reduce that, but it hasn’t been a concern.
Q. Do goroutine stacks adapt in size?
The initial stack allocated for a goroutine does not adapt. It’s always 4k right now. It has been other values in the past but always a constant. One of the things I’d like to do is to look at what the goroutine will be running and adjust the stack accordingly, but I haven’t.
Q. Are there any short-term plans for dynamic loading of modules?
No. I don’t think there are any technical surprises, but assuming that everything is statically linked simplified some of the implementation. Like with calling Go from C++ programs, I believe it’s just work.
Gccgo might be closer to support for this, but I don’t believe that it supports dynamic loading right now either.
Q. How much does the language spec say about reflection?
The spec is intentionally vague about reflection, but package reflect’s API is definitely part of the Go 1 definition. Any conforming implementation would need to implement that API. In fact, gc and gccgo do have different implementations of that package reflect API, but then the packages that use reflect like fmt and json can be shared.
Q. Do you have a release schedule?
We don’t have any fixed release schedule. We’re not keeping things secret, but we’re also not making commitments to specific timelines.
Go 1 was in progress publicly for months, and if you watched you could see the bug count go down and the release candidates announced, and so on.
Right now we’re trying to slow down. We want people to write things using Go, which means we need to make it a stable foundation to build on. Go 1.0.1, the first bug release, was released four weeks after Go 1, and Go 1.0.2 was seven weeks after Go 1.0.1.
Q. Where do you see Go in five years? What languages will it replace?
I hope that it will still be at golang.org, that the Go project will still be thriving and relevant. We built it to write the kinds of programs we’ve been writing in C++, Java, and Python, but we’re not trying to go head-to-head with those languages. Each of those has definite strengths that make them the right choice for certain situations. We think that there are plenty of situations, though, where Go is a better choice.
If Go doesn’t work out, and for some reason in five years we’re programming in something else, I hope the something else would have the features I talked about, specifically the Go way of doing interfaces and the Go way of handling concurrency.
If Go fails but some other language with those two features has taken over the programming landscape, if we can move the computing world to a language with those two features, then I’d be sad about Go but happy to have gotten to that situation.
Q. What are the limits to scalability with building a system with many goroutines?
The primary limit is the memory for the goroutines. Each goroutine starts with a 4kB stack and a little more per-goroutine data, so the overhead is between 4kB and 5kB. That means on this laptop I can easily run 100,000 goroutines, in 500 MB of memory, but a million goroutines is probably too much.
For a lot of simple goroutines, the 4 kB stack is probably more than necessary. If we worked on getting that down we might be able to handle even more goroutines. But remember that this is in contrast to C threads, where 64 kB is a tiny stack and 1-4MB is more common.
Q. How would you build a traditional barrier using channels?
It’s important to note that channels don’t attempt to be a concurrency Swiss army knife. Sometimes you do need other concepts, and the standard sync package has some helpers. I’d probably use a sync.WaitGroup.
If I had to use channels, I would do it like in the web crawler example, with a channel that all the goroutines write to, and a coordinator that knows how many responses it expects.
Q. What is an example of the kind of application you’re working on performance for? How will you beat C++?
I haven’t been focusing on specific applications. Go is still young enough that if you run some microbenchmarks you can usually find something to optimize. For example, I just sped up floating point computation by about 25% a few weeks ago. I’m also working on more sophisticated analyses for things like escape analysis and bounds check elimination, which address problems that are unique to Go, or at least not problems that C++ faces.
Our goal is definitely not to beat C++ on performance. The goal for Go is to be near C++ in terms of performance but at the same time be a much more productive environment and language, so that you’d rather program in Go.
Q. What are the security features of Go?
Go is a type-safe and memory-safe language. There are no dangling pointers, no pointer arithmetic, no use-after-free errors, and so on.
You can break the rules by importing package unsafe, which gives you a special type unsafe.Pointer. You can convert any pointer or integer to an unsafe.Pointer and back. That’s the escape hatch, which you need sometimes, like for extracting the bits of a float64 as a uint64. But putting it in its own package means that unsafe code is explicitly marked as unsafe. If your program breaks in a strange way, you know where to look.
Isolating this power also means that you can restrict it. On App Engine you can’t import package unsafe in the code you upload for your app.
I should point out that the current Go implementation does have data races, but they are not fundamental to the language. It would be possible to eliminate the races at some cost in efficiency, and for now we’ve decided not to do that. There are also tools such as Thread Sanitizer that help find these kinds of data races in Go programs.
Q. What language do you think Go is trying to displace?
I don’t think of Go that way. We were writing C++ code before we did Go, so we definitely wanted not to write C++ code anymore. But we’re not trying to displace all C++ code, or all Python code, or all Java code, except maybe in our own day-to-day work.
One of the surprises for me has been the variety of languages that new Go programmers used to use. When we launched, we were trying to explain Go to C++ programmers, but many of the programmers Go has attracted have come from more dynamic languages like Python or Ruby.
Q. How does Go make it possible to use multiple cores?
Go lets you tell the runtime how many operating system threads to use for executing goroutines, and then it muxes the goroutines onto those threads. So if you’ve written a program that has four or more goroutines executing simultaneously, you can tell the runtime to use four OS threads and then you’re running on four cores.
We’ve been pleasantly surprised by how easy people find it to write these kinds of programs. People who have not written parallel or concurrent programs before write concurrent Go programs using channels that can take advantage of multiple cores, and they enjoy the experience. That’s more than you can usually say for C threads. Joe Armstrong, one of the creators of Erlang, makes the point that thinking about concurrency in terms of communication might be more natural for people, since communication is something we’ve done for a long time. I agree.
Q. How does the muxing of goroutines work?
It’s not very smart. It’s the simplest thing that isn’t completely stupid: all the scheduling operations are O(1), and so on, but there’s a shared run queue that the various threads pull from. There’s no affinity between goroutines and threads, there’s no attempt to make sophisticated scheduling decisions, and there’s not even preemption.
The goroutine scheduler was the first thing I wrote when I started working on Go, even before I was working full time on it, so it’s just about four years old. It has served us surprisingly well, but we’ll probably want to replace it in the next year or so. We’ve been having some discussions recently about what we’d want to try in a new scheduler.
Q. Is there any plan to bootstrap Go in Go, to write the Go compiler in Go?
There’s no immediate plan. Go does ship with a Go program parser written in Go, so the first piece is already done, and there’s an experimental type checker in the works, but those are mainly for writing program analysis tools. I think that Go would be a great language to write a compiler in, but there’s no immediate plan. The current compiler, written in C, works well.
I’ve worked on bootstrapped languages in the past, and I found that bootstrapping is not necessarily a good fit for languages that are changing frequently. It reminded me of climbing a cliff and screwing hooks into the cliff once in a while to catch you if you fall. Once or twice I got into situations where I had identified a bug in the compiler, but then trying to write the code to fix the bug tickled the bug, so it couldn’t be compiled. And then you have to think hard about how to write the fix in a way that avoids the bug, or else go back through your version control history to find a way to replay history without introducing the bug. It’s not fun.
The fact that Go wasn’t written in itself also made it much easier to make significant language changes. Before the initial release we went through a handful of wholesale syntax upheavals, and I’m glad we didn’t have to worry about how we were going to rebootstrap the compiler or ensure some kind of backwards compatibility during those changes.
Finally, I hope you’ve read Ken Thompson’s Turing Award lecture, Reflections on Trusting Trust. When we were planning the initial open source release, we liked to joke that no one in their right mind would accept a bootstrapped compiler binary written by Ken.
Q. What does Go do to compile efficiently at scale?
This is something that we talked about a lot in early talks about Go. The main thing is that it cuts off transitive dependencies when compiling a single module. In most languages, if package A imports B, and package B imports C, then the compilation of A reads not just the compiled form of B but also the compiled form of C. In large systems, this gets out of hand quickly. For example, in C++ on my Mac, including <iostream> reads 25,326 lines from 131 files. (C and C++ headers aren't “compiled form,” but the problem is the same.) Go promises that each import reads a single compiled package file. If you need to know something about other packages to understand that package’s API, then the compiled file includes the extra information you need, but only that.
Of course, if you are building from scratch and package A imports B which imports C, then of course C has to be compiled first, and then B, and then A. The import point is that when you go to compile A, you don’t reload C’s object file. In a real program, the dependencies are usually not a chain like this. We might have A1, A2, A3, and so on all importing B. It’s a significant win if none of them need to reread C.
Q. How do you identify a good project for Go?
I think a good project for Go is one that you’re excited about writing in Go. Go really is a general purpose programming language, and except for the compiler work, it’s the only language I’ve written significant programs in for the past four years.
Most of the people I know who are using Go are using it for networked servers, where the concurrency features have something contribute, but it’s great for other contexts too. I’ve used it to write a simple mail reader, file system implementations to read old disks, and a variety of other unnetworked programs.
Q. What is the current and future IDE support for Go?
I’m not an IDE user in the modern sense, so really I don’t know. We think that it would be possible to write a really nice IDE specifically for Go, but it’s not something we’ve had time to explore. The Go distribution has a misc directory that contains basic Go support for common editors, and there is a Goclipse project to write an Eclipse-based IDE, but I don’t know much about those.
The development environment I use, acme, is great for writing Go code, but not because of any custom Go support.
If you have more questions, please consult these resources.
May 25, 2012
newsham
The great latency race
You can make more money on wall street if you can get your orders into the queue first.
That statement is a gross oversimplification, but there is truth to it. Enough truth to cause wall street to hire lots of really really smart people to make their systems run ever so slightly faster. Enough truth to cause wall street to move computers from one location to another location just so that they don't have to wait for electronic signals to travel the longer distance. This is a pretty amazing thing! We've incentivized wall street to waste huge amounts of resources on something that shouldn't really matter. The market is a very important (and very impressive!) arbiter of our economic system and it provides great benefits to our society. The "latency race" to get orders into the order books is not one of them. Nor are the incentives that created the "latency race" a necessary part of the system.
One way we could eliminate the incentives that led to this madness is with a lottery. First pick a time quantum, say 1ms. Next change the order processing to batch together all orders received in the same time quantum that have matching prices into a pool. At the end of that quantum process the orders in a random order. In effect create a lottery for all orders placed "at the same time." Order processing proceeds as before; the only difference is that orders at the same price are processed in lottery order instead of first-come-first-serve order. Suddenly there is no need to make automated trading software work any faster than the time quantum. The pointless "latency race" is put to rest.
May 20, 2012
Stanley Lieber
(Untitled)
stanleylieber posted a photo:
(Untitled)
stanleylieber posted a photo:
(Untitled)
stanleylieber posted a photo:
(Untitled)
stanleylieber posted a photo:
(Untitled)
stanleylieber posted a photo:
turned out to be a photocopy.
stanleylieber posted a photo:
(Untitled)
stanleylieber posted a photo:
(Untitled)
stanleylieber posted a photo:
May 15, 2012
May 10, 2012
Software Magpie

Terminal madness
Tonight I was updating an Ubuntu server to 12.04LTS using
do-release-upgrade.
It failed, because of a problem with my locale. Normally I use LANG=C to avoid some unpleasantness for a programming environment, but it was set to en_GB.UTF-8, which confused the libc update, aborting the upgrade and leaving the system in a highly inconsistent state. Wonderful.
A quick Google found a way round it:
apt-get -o APT::Immediate-Configure=0 -f install
which was fine (no, I've no idea either), and I'd set LANG=C just in case, but because I was using 9term, the apt-get initially failed with:
Unknown terminal: 9term
Check the TERM environment variable.
Also make sure that the terminal is defined in the terminfo database.
Alternatively, set the TERMCAP environment variable to the desired termcap entry.
debconf: whiptail output the above errors, giving up!
May 08, 2012
Stanley Lieber
hp 8100c, *msi=1, *nousbehci=1, *nousbuhci=1
stanleylieber posted a photo:
April 20, 2012
April 17, 2012
Stanley Lieber
(Untitled)
stanleylieber posted a photo:
(Untitled)
stanleylieber posted a photo:
(Untitled)
stanleylieber posted a photo:
(Untitled)
stanleylieber posted a photo:
(Untitled)
stanleylieber posted a photo:
April 16, 2012
April 12, 2012
research!rsc

QArt Codes
QR codes are 2-dimensional bar codes that encode arbitrary text strings. A common use of QR codes is to encode URLs so that people can scan a QR code (for example, on an advertising poster, building roof, volleyball bikini, belt buckle, or airplane banner) to load a web site on a cell phone instead of having to “type” in a URL.
QR codes are encoded using Reed-Solomon error-correcting codes, so that a QR scanner does not have to see every pixel correctly in order to decode the content. The error correction makes it possible to introduce a few errors (fewer than the maximum that the algorithm can fix) in order to make an image. For example, in 2008, Duncan Robertson took a QR code for “http://bbc.co.uk/programmes” (left) and introduced errors in the form of a BBC logo (right):

That's a neat trick and a pretty logo, but it's uninteresting from a technical standpoint. Although the BBC logo pixels look like QR code pixels, they are not contribuing to the QR code. The QR reader can't tell much difference between the BBC logo and the Union Jack. There's just a bunch of noise in the middle either way.

Since the BBC QR logo appeared, there have been many imitators. Most just slap an obviously out-of-place logo in the middle of the code. This Disney poster is notable for being more in the spirit of the BBC code.
There's a different way to put pictures in QR codes. Instead of scribbling on redundant pieces and relying on error correction to preserve the meaning, we can engineer the encoded values to create the picture in a code with no inherent errors, like these:




This post explains the math behind making codes like these, which I call QArt codes. I have published the Go programs that generated these codes at code.google.com/p/rsc and created a web site for creating these codes.
Background
For error correction, QR uses Reed-Solomon coding (like nearly everything else). For our purposes, Reed-Solomon coding has two important properties. First, it is what coding theorists call a systematic code: you can see the original message in the encoding. That is, the Reed-Solomon encoding of “hello” is “hello” followed by some error-correction bytes. Second, Reed-Solomon encoded messages can be XOR'ed: if we have two different Reed-Solomon encoded blocks b1 and b2 corresponding to messages m1 and m2, b1 ⊕ b2 is also a Reed-Solomon encoded block; it corresponds to the message m1 ⊕ m2. (Here, ⊕ means XOR.) If you are curious about why these two properties are true, see my earlier post, Finite Field Arithmetic and Reed-Solomon Coding.
QR Codes
A QR code has a distinctive frame that help both people and computers recognize them as QR codes. The details of the frame depend on the exact size of the code—bigger codes have room for more bits—but you know one when you see it: the outlined squares are the giveaway. Here are QR frames for a sampling of sizes:

The colored pixels are where the Reed-Solomon-encoded data bits go. Each code may have one or more Reed-Solomon blocks, depending on its size and the error correction level. The pictures show the bits from each block in a different color. The L encoding is the lowest amount of redundancy, about 20%. The other three encodings increase the redundancy, using 38%, 55%, and 65%.

(By the way, you can read the redundancy level from the top pixels in the two leftmost columns. If black=0 and white=1, then you can see that 00 is L, 01 is M, 10 is Q, and 11 is H. Thus, you can tell that the QR code on the T-shirt in this picture is encoded at the highest redundancy level, while this shirt uses the lowest level and therefore might take longer or be harder to scan.
As I mentioned above, the original message bits are included directly in the message's Reed-Solomon encoding. Thus, each bit in the original message corresponds to a pixel in the QR code. Those are the lighter pixels in the pictures above. The darker pixels are the error correction bits. The encoded bits are laid down in a vertical boustrophedon pattern in which each line is two columns wide, starting at the bottom right corner and ending on the left side:

We can easily work out where each message bit ends up in the QR code. By changing those bits of the message, we can change those pixels and draw a picture. There are, however, a few complications that make things interesting.
QR Masks
The first complication is that the encoded data is XOR'ed with an obfuscating mask to create the final code. There are eight masks:

An encoder is supposed to choose the mask that best hides any patterns in the data, to keep those patterns from being mistaken for framing boxes. In our encoder, however, we can choose a mask before choosing the data. This violates the spirit of the spec but still produces legitimate codes.
QR Data Encoding
The second complication is that we want the QR code's message to be intelligible. We could draw arbitrary pictures using arbitrary 8-bit data, but when scanned the codes would produce binary garbage. We need to limit ourselves to data that produces sensible messages. Luckily for us, QR codes allow messages to be written using a few different alphabets. One alphabet is 8-bit data, which would require binary garbage to draw a picture. Another is numeric data, in which every run of 10 bits defines 3 decimal digits. That limits our choice of pixels slightly: we must not generate a 10-bit run with a value above 999. That's not complete flexibility, but it's close: 9.96 bits of freedom out of 10. If, after encoding an image, we find that we've generated an invalid number, we pick one of the 5 most significant bits at random—all of them must be 1s to make an invalid number—hard wire that bit to zero, and start over.
Having only decimal messages would still not be very interesting: the message would be a very large number. Luckily for us (again), QR codes allow a single message to be composed from pieces using different encodings. The codes I have generated consist of an 8-bit-encoded URL ending in a # followed by a numeric-encoded number that draws the actual picture:
The leading URL is the first data encoded; it takes up the right side of the QR code. The error correction bits take up the left side.
When the phone scans the QR code, it sees a URL; loading it in a browser visits the base page and then looks for an internal anchor on the page with the given number. The browser won't find such an anchor, but it also won't complain.
The techniques so far let us draw codes like this one:


The second copy darkens the pixels that we have no control over: the error correction bits on the left and the URL prefix on the right. I appreciate the cyborg effect of Peter melting into the binary noise, but it would be nice to widen our canvas.
Gauss-Jordan Elimination
The third complication, then, is that we want to draw using more than just the slice of data pixels in the middle of the image. Luckily, we can.
I mentioned above that Reed-Solomon messages can be XOR'ed: if we have two different Reed-Solomon encoded blocks b1 and b2 corresponding to messages m1 and m2, b1 ⊕ b2 is also a Reed-Solomon encoded block; it corresponds to the message m1 ⊕ m2. (In the notation of the previous post, this happens because Reed-Solomon blocks correspond 1:1 with multiples of g(x). Since b1 and b2 are multiples of g(x), their sum is a multiple of g(x) too.) This property means that we can build up a valid Reed-Solomon block from other Reed-Solomon blocks. In particular, we can construct the sequence of blocks b0, b1, b2, ..., where bi is the block whose data bits are all zeros except for bit i and whose error correction bits are then set to correspond to a valid Reed-Solomon block. That set is a basis for the entire vector space of valid Reed-Solomon blocks. Here is the basis matrix for the space of blocks with 2 data bytes and 2 checksum bytes:
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||||||
| 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||||
The missing entries are zeros. The gray columns highlight the pixels we have complete control over: there is only one row with a 1 for each of those pixels. Each time we want to change such a pixel, we can XOR our current data with its row to change that pixel, not change any of the other controlled pixels, and keep the error correction bits up to date.
So what, you say. We're still just twiddling data bits. The canvas is the same.
But wait, there's more! The basis we had above lets us change individual data pixels, but we can XOR rows together to create other basis matrices that trade data bits for error correction bits. No matter what, we're not going to increase our flexibility—the number of pixels we have direct control over cannot increase—but we can redistribute that flexibility throughout the image, at the same time smearing the uncooperative noise pixels evenly all over the canvas. This is the same procedure as Gauss-Jordan elimination, the way you turn a matrix into row-reduced echelon form.
This matrix shows the result of trying to assert control over alternating pixels (the gray columns):
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||||||
| 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||||
| 1 | 1 | 1 | 1 | ||||||||||||||||||||||||||||
The matrix illustrates an important point about this trick: it's not completely general. The data bits are linearly independent, but there are dependencies between the error correction bits that mean we often can't have every pixel we ask for. In this example, the last four pixels we tried to get were unavailable: our manipulations of the rows to isolate the first four error correction bits zeroed out the last four that we wanted.
In practice, a good approach is to create a list of all the pixels in the Reed-Solomon block sorted by how useful it would be to be able to set that pixel. (Pixels from high-contrast regions of the image are less important than pixels from low-contrast regions.) Then, we can consider each pixel in turn, and if the basis matrix allows it, isolate that pixel. If not, no big deal, we move on to the next pixel.
Applying this insight, we can build wider but noisier pictures in our QR codes:


The pixels in Peter's forehead and on his right side have been sacrificed for the ability to draw the full width of the picture.
We can also choose the pixels we want to control at random, to make Peter peek out from behind a binary fog:



Rotations
One final trick. QR codes have no required orientation. The URL base pixels that we have no control over are on the right side in the canonical orientation, but we can rotate the QR code to move them to other edges.




Further Information
All the source code for this post, including the web server, is at code.google.com/p/rsc/source/browse/qr. If you liked this, you might also like Zip Files All The Way Down.
Acknowledgements
Alex Healy pointed out that valid Reed-Solomon encodings are closed under XOR, which is the key to spreading the picture into the error correction pixels. Peter Weinberger has been nothing but gracious about the overuse of his binary likeness. Thanks to both.
April 10, 2012
research!rsc

Finite Field Arithmetic and Reed-Solomon Coding
Finite fields are a branch of algebra formally defined in the 1820s, but interest in the topic can be traced back to public sixteenth-century polynomial-solving contests. For the next few centuries, finite fields had little practical value, but all changed in the last fifty years. It turns out that they are useful for many applications in modern computing, such as encryption, data compression, and error correction.
In particular, Reed-Solomon codes are an error-correcting code based on finite fields and used everywhere today. One early significant use was in the Voyager spacecraft: the messages it still sends back today, from the edge of the solar system, are heavily Reed-Solomon encoded so that even if only a small fragment makes it back to Earth, we can still reconstruct the message. Reed-Solomon coding is also used on CDs to withstand scratches, in wireless communications to withstand transmission problems, in QR codes to withstand scanning errors or smudges, in disks to withstand loss of fragments of the media, in high-level storage systems like Google's GFS and BigTable to withstand data loss and also to reduce read latency (the read can complete without waiting for all the responses to arrive).
This post shows how to implement finite field arithmetic efficiently on a computer, and then how to use that to implement Reed-Solomon encoding.
What is a Finite Field?
One way mathematicians study numbers is to abstract away the numbers themselves and focus on the operations. (This is kind of an object-oriented approach to math.) A field is defined as a set F and operators + and · on elements of F that satisfy the following properties:
- (Closure) For all x, y in F, x+y and x·y are in F.
- (Associative) For all x, y, z in F, (x+y)+z = x+(y+z) and (x·y)·z = x·(y·z).
- (Commutative) For all x, y in F, x+y = y+x and x·y = y·x.
- (Distributive) For all x, y, z in F, x·(y+z) = (x·y)+(x·z).
- (Identity) There is some element we'll call 0 in F such that for all x in F, x+0 = x. Similarly, there is some element we'll call 1 in F such that for all x in F, x·1 = x.
- (Inverse) For all x in F, there is some element y in F such that x+y = 0. We write y = −x. Similarly, for all x in F except 0, there is some element y in F such that x·y = 1. We write y = 1/x.
You probably recognize those properties from high school algebra class: the most well-known example of a field is the real numbers, where + is addition and · is multiplication. Other examples are complex numbers and fractions.
A mathematician doesn't have to prove the same results over and over
for the real numbers ℝ, the complex numbers ℂ, the fractions ℚ, and so on.
Instead, she can prove that a particular result holds for all fields—by assuming only
the above properties, called the field axioms. Then she can apply the result by
substituting a specific instance like the real numbers for the general idea of a field,
the same way that a programmer can implement just one vector(T)
and then instantiate it as vector(int), vector(string) and so on.
The integers ℤ are not a field: they lack multiplicative inverses. For example, there is no number that you can multiply by 2 to get 1, no 1/2. Surprisingly, though, the integers modulo any prime p do form a field. For example, the integers modulo 5 are 0, 1, 2, 3, 4. 1+4 = 0 (mod 5), so we say that 4 = −1. Similarly, 2·3 = 1 (mod 5), so we say that 3 = 1/2. After we've proved that ℤ/p is in fact a field, all the results about fields can be applied to ℤ/p. This is very useful: it lets us apply our intuition about the very familiar real numbers to these less familiar numbers. This field is written ℤ/p to emphasize that we're dealing with what's left after subtracting out all the p's. That is, we're dealing with what's left if you assume that p = 0. When you make that assumption, you get math that wraps around at p. These fields are called finite fields because, in contrast to fields like the real numbers, they have a finite number of elements.
For a programmer, the most interesting finite field is
ℤ/2, which contains just the integers 0, 1. Addition
is the same as XOR, and multiplication is the same as AND.
Note that ℤ/p is only a field when p is prime:
arithmetic on uint8 variables corresponds
to ℤ/256, but it is not a field: there is no 1/2.
What can you do with a field?
The only problem with fields is that there's not a ton you can do with just the field axioms. One thing you can do is build polynomials, which were the original motivation for the mathematicians who pioneered the use of fields in the early 1800s. If we introduce a symbolic variable x, then we can build polynomials whose coefficients are field values. We'll write F[x] to denote the polynomials over x using coefficients from F. For example, if we use the real numbers ℝ as our field, then the polynomials ℝ[x] include x2+1, x+2, and 3.14x2 − 2.72x + 1.41. Like integers, these polynomials can be added and multiplied, but not always divided—what is (x2+1)/(x+2)?—so they are not a field. However, remember how the integers are not a field but the integers modulo a prime are a field? The same happens here: polynomials are not a field but polynomials modulo some prime polynomial are.
What does “polynomials modulo some prime polynomial” mean anyway? A prime polynomial is one that cannot be factored, like x2+1 cannot be factored using real numbers. The field ℤ/5 is what you get by doing math under the assumption that 5 = 0; similarly, ℝ[x]/(x2+1) is what you get by doing math under the assumption that x2+1 = 0. Just as ℤ/5 math never deals with numbers as big as 5, ℝ[x]/(x2+1) math never deals with polynomials as big as x2: anything bigger can have some multiple of x2+1 subtracted out again. That is, the polynomials in ℝ[x]/(x2+1) are bounded in size: they have only x1 and x0 (constant) terms. To add polynomials, we just add the coefficients using the addition rule from the coefficient's field, independently, like a vector addition. To multiply polynomials, we have to do the multiplication and then subtract out any x2+1 we can. If we have (ax+b)·(cx+d), we can expand this to (a·c)x2 + (b·c+a·d)x + (b·d), and then subtract (a·c)(x2+1) = (a·c)x2 + (a·c), producing the final result: (b·c+a·d)x + (b·d−a·c). That might seem like a funny definition of multiplication, but it does in fact obey the field axioms. In fact, this particular field is more familiar than it looks: it is the complex numbers ℂ, but we've written x instead of the usual i. Assuming that x2+1 = 0 is, except for a renaming, the same as defining i2 = −1.
Doing all our math modulo a prime polynomial let us take the field of real numbers and produce a field whose elements are pairs of real numbers. We can apply the same trick to take a finite field like ℤ/p and product a field whose elements are fixed-length vectors of elements of ℤ/p. The original ℤ/p has p elements. If we construct (ℤ/p)[x]/f(x), where f(x) is a prime polynomial of degree n (f's maximum x exponent is n), the resulting field has pn elements: all the vectors made up of n elements from ℤ/p. Incredibly, the choice of prime polynomial doesn't matter very much: any two finite fields of size pn have identical structure, even if they give the individual elements different names. Because of this, it makes sense to refer to all the finite fields of size pn as one concept: GF(pn). The GF stands for Galois Field, in honor of Évariste Galois, who was the first to study these. The exact polynomial chosen to produce a particular GF(pn) is an implementation detail.
For a programmer, the most interesting finite fields constructed this way are GF(2n)—the polynomial extensions of ℤ/2—because the elements of GF(2n) are bit vectors of length n. As a concrete example, consider (ℤ/2)[x]/(x8+x4+x3+x+1) . The field has 28 elements: each can be represented by a single byte. The byte with binary digits b7b6b5b4b3b2b1b0 represents the polynomial b7·x7 + b6·x6 + b5·x5 + b4·x4 + b3·x3 + b2·x2 + b1·x1 + b0. To add polynomials, we add coefficients. Since the coefficients are from ℤ/2, adding coefficients means XOR'ing each bit position separately, which is something computer hardware can do easily. Multiplying the polynomials is more difficult, because standard multiplication hardware is based on adding, but we need a multiplication based on XOR'ing. Because the coefficient math wraps at 2, (x2+x)·(x+1) = x3+2x2+x = x3+x, while computer multiplication would choose 1102* 0112 = 6 * 3 = 18 = 100102. However, it turns out that we can implement this field multiplication with a simple lookup table. In a finite field, there is always at least one element α that can serve as a generator. All the other non-zero elements are powers of α: α, α2, α3, and so on. This α is not symbolic like x: it's a specific element. For example, in ℤ/5, we can use α=2: {α, α2, α3, α4} = {2, 4, 8, 16} = {2, 4, 3, 1}. In GF(2n) the math is more complex but still works. If we know the generator, then we can, by repeated multiplication, create a lookup table exp[i] = αⁱ and an inverse table log[αⁱ] = i. Multiplication is then just a few table lookups: assuming a and b are non-zero, a·b = exp[log[a]+log[b]]. (That's a normal integer +, to add the exponents, not an XOR.)
Why do we care?
The fact that GF(2n) can be implemented efficiently on a computer means that we can implement systems based on mathematical theorems without worrying about the usual overflow problems you get when modeling integers or real numbers. To be sure, GF(2n) behaves quite differently from the integers in many ways, but if all you need is the field axioms, it's good enough, and it eliminates any need to worry about overflow or arbitrary precision calculations. Because of the lookup table, GF(28) is by far the most common choice of field in a computer algorithm. For example, the Advanced Encryption Standard (AES, formerly Rijndael) is built around GF(28) arithmetic, as are nearly all implementations of Reed-Solomon coding.
Code
Let's begin by defining a Field type that will
represent the specific instance of GF(28) defined by a
given polynomial.
The polynomial must be of degree 8, meaning that
its binary representation has the 0x100 bit set and no
higher bits set.
type Field struct {
...
}
Addition is just XOR, no matter what the polynomial is:
// Add returns the sum of x and y in the field.
func (f *Field) Add(x, y byte) byte {
return x ^ y
}
Multiplication is where things get interesting. If you'd used binary (and Go) in grade school, you might have learned this algorithm for multiplying two numbers (this is not finite field arithmetic):
// Grade-school multiplication in binary: mul returns the product x×y.
func mul(x, y int) int {
z := 0
for x > 0 {
if x&1 != 0 {
z += y
}
x >>= 1
y <<= 1
}
return z
}
The running total z accumulates the product of x and y.
The first iteration of this loop adds y to z if the
low bit (the 1s digit) of x is 1.
The next iteration adds y*2 if the next bit (the 2s digit, now shifted down) of
x is 1.
The next iteration adds y*4 if the 4s digit is 1, and so on.
Each iteration shifts x to the right to chop off the processed digit
and shifts y to the left to multiply by two.
To adapt this to multiply in a finite field, we need to make two changes.
First, addition is XOR, so we use ^= instead of +=
to add to z.
Second, we need to make the multiply reduce modulo the polynomial.
Assuming that the inputs have already been reduced, the only chance
of exceeding the polynomial comes from the shift of y.
After the shift, then, we can check to see if we've overflowed, and if so,
subtract (XOR) out one copy of the polynomial.
The finite field version, then, is:
// GF(256) mutiplication: mul returns the product x×y mod poly.
func mul(x, y, poly int) int {
z := 0
for x > 0 {
if x&1 != 0 {
z ^= y
}
x >>= 1
y <<= 1
if y&0x100 != 0 {
y ^= poly
}
}
return z
}
We might want to do a lot of multiplication, though,
and this loop is too slow. There aren't that many inputs—only 28×28 of them—so one
option is to build a 64kB lookup table. With some cleverness, we can
build a smaller lookup table.
In the NewField
constructor, we can compute α0, α1, α2, ..., record the sequence
in an exp array, and record the inverse in
a log array.
Then we can reduce multiplication to addition of logarithms,
like a slide rule does.
// A Field represents an instance of GF(256) defined by a specific polynomial.
type Field struct {
log [256]byte // log[0] is unused
exp [510]byte
}
// NewField returns a new field corresponding to
// the given polynomial and generator.
func NewField(poly, α int) *Field {
var f Field
x := 1
for i := 0; i < 255; i++ {
f.exp[i] = byte(x)
f.exp[i+255] = byte(x)
f.log[x] = byte(i)
x = mul(x, α, poly)
}
f.log[0] = 255
return &f
}
The values of the exp function cycle with period 255
(not 256, because 0 is impossible): α255 = 1.
The straightforward way to implement Exp, then,
is to look up the entry given by the exponent modulo 255.
// Exp returns the base 2 exponential of e in the field.
// If e < 0, Exp returns 0.
func (f *Field) Exp(e int) byte {
if e < 0 {
return 0
}
return f.exp[e%255]
}
Log is an even simpler table lookup, because the input
is only a byte:
// Log returns the base 2 logarithm of x in the field.
// If x == 0, Log returns -1.
func (f *Field) Log(x byte) int {
if x == 0 {
return -1
}
return int(f.log[x])
}
Mul is where things get interesting.
The obvious implementation of Mul is exp[(log[x]+log[y])%255],
but if we double the exp array, so that it is 510 elements long,
we can drop the relatively expensive %255:
// Mul returns the product of x and y in the field.
func (f *Field) Mul(x, y byte) byte {
if x == 0 || y == 0 {
return 0
}
return f.exp[int(f.log[x])+int(f.log[y])]
}
Inv returns the multiplicative inverse, 1/x.
We don't implement divide: instead of x/y, we can use x · 1/y.
// Inv returns the multiplicative inverse of x in the field.
// If x == 0, Inv returns 0.
func (f *Field) Inv(x byte) byte {
if x == 0 {
return 0
}
return f.exp[255-f.log[x]]
}
Reed-Solomon Coding
In 1960, Irving Reed and Gustave Solomon proposed a way to build an error-correcting code using GF(2n). The method interpreted the m message bits as coefficients of a polynomial f of degree m−1 over GF(2n) and then sent f(0), f(α), f(α2), f(α3), ..., f(1). Any m of these, if received correctly, suffice to reconstruct f, and then the message can be read off the coefficients. To find a correct set, Reed and Solomon's algorithm constructed the f corresponding to every possible subset of m received values and then chose the most common one in a majority vote. As long as no more than (2n−m)/2 values were corrupted in transit, the majority will agree on the correct value of f. This decoding algorithm is very expensive, too expensive for long messages. As a result, the Reed-Solomon approach sat unused for almost a decade. In 1969, however, Elwyn Berlekamp and James Massey proposed a variant with an efficient decoding algorithm. In the 1980s, Berlekamp and Lloyd Welch developed an even more efficient decoding algorithm that is the one typically used today. These decoding algorithms are based on systems of equations far too complex to explain here; in this post, we will only deal with encoding. (I can't keep the decoding algorithms straight in my head for more than an hour or two at a time, much less explain them in finite space.)
In Reed-Solomon encoding as it is practiced today, the choice of finite field F and generator α defines a generator polynomial g(x) = (x−1)(x−α)(x−α2)...(x−αn−m). To encode a message m, the message is taken as the top coefficients of a degree n polynomial f(x) = m0xn−1+m1xn−2+...+mmxn−m−1. Then that polynomial can be divided by g to produce the remainder polynomial r(x), the unique polynomial of degree less than n−m such that f(x) − r(x) is a multiple of g(x). Since r(x) is of degree less than n−m, subtracting r(x) does not affect any of the message coefficients, just the lower terms, so the polynomial f(x) − r(x) (= f(x) + r(x)) is taken as the encoded message. All encoded messages, then, are multiples of g(x). On the receiving end, the decoder does some magic to figure out the simplest changes needed to make the received polynomial a multiple of g(x) and then reads the message out of the top coefficients.
While decoding is difficult, encoding is easy: the first m bytes are the message itself, followed by the c bytes defining the remainder of m·xc/g(x). We can also check whether we received an error-free message by checking whether the concatenation defines a polynomial that is a multiple of g(x).
Code
The Reed-Solomon encoding problem is this: given a message m interpreted as a polynomial m(x), compute the error correction bytes, m(x)·xc mod g(x).
The grade-school division algorithm works well here.
If we fill in p with m(x)·xc (m followed by c zero bytes),
then we can replace p by the remainder by iteratively subtracting out
multiples of the generator polynomial g.
for i := 0; i < len(m); i++ {
k := f.Mul(p[i], f.Inv(gen[0])) // k = pi / g0
// p -= k·g
for j, g := range gen {
p[i+j] = f.Add(p[i+j], f.Mul(k, g))
}
}
This implementation is correct but can be made more efficient. If you want to try, run:
go get code.google.com/p/rsc/gf256 go test code.google.com/p/rsc/gf256 -bench Blog
That benchmark measures
the speed of the implementation in blog_test.go,
which looks like the above. Optimize away, or follow along.
There's definitely room for improvement:
$ go test code.google.com/p/rsc/gf256 -bench ECC PASS BenchmarkBlogECC 500000 7031 ns/op 4.55 MB/s BenchmarkECC 1000000 1332 ns/op 24.02 MB/s
To start, we can expand the definitions of Add and Mul.
The Go compiler's inliner would do this for us; the win here is not
the inlining but the simplifications it will enable us to make.
for i := 0; i < len(m); i++ {
if p[i] == 0 {
continue
}
k := f.exp[f.log[p[i]] + 255 - f.log[gen[0]]] // k = pi / g0
// p -= k·g
for j, g := range gen {
p[i+j] ^= f.exp[f.log[k] + f.log[g]]
}
}
(The implementation handles p[i] == 0 specially
because 0 has no log.)
The first thing to note is that we compute k but then use
f.log[k] repeatedly. Computing the log will avoid that
memory access, and it is cheaper: we just take out the f.exp[...] lookup
on the line that computes k. This is safe because p[i] is non-zero, so k must be non-zero.
for i := 0; i < len(m); i++ {
if p[i] == 0 {
continue
}
lk := f.log[p[i]] + 255 - f.log[gen[0]] // k = pi / g0
// p -= k·g
for j, g := range gen {
p[i+j] ^= f.exp[lk + f.log[g]]
}
}
Next, note that we repeatedly compute f.log[g]. Instead of doing that,
we can iterate lgen—an array holding the logs of the coefficients—instead of gen.
We'll have to handle zero somehow: let's say that the array has an entry set to 255
when the corresponding gen value is zero.
for i := 0; i < len(m); i++ {
if p[i] == 0 {
continue
}
lk := f.log[p[i]] + 255 - f.log[gen[0]] // k = pi / g0
// p -= k·g
for j, lg := range lgen {
if lg != 255 {
p[i+j] ^= f.exp[lk + lg]
}
}
}
Next, we can notice that since the generator is defined as
the first coefficient, g0, is always 1! That means we can simplify the k = pi / g calculation to just k = pi. Also, we can drop the first element of lgen and its subtraction, as long as we ignore the high bytes in the result (we know they're supposed to be zero anyway).
for i := 0; i < len(m); i++ {
if p[i] == 0 {
continue
}
lk := f.log[p[i]]
// p -= k·g
for j, lg := range lgen {
if lg != 255 {
p[i+1+j] ^= f.exp[lk + lg]
}
}
}
The inner loop, which is where we spend all our time, has two
additions by loop-invariant constants: i+1+j and lk+lg.
The i+1 and lk do not change on each iteration.
We can avoid those additions by reslicing the arrays
outside the loop:
for i := 0; i < len(m); i++ {
if p[i] == 0 {
continue
}
lk := f.log[p[i]]
// p -= k·g
q := p[i+1:]
exp := f.exp[lk:]
for j, lg := range lgen {
if lg != 255 {
q[j] ^= exp[lg]
}
}
}
As one final trick, we can replace p[i] by a range variable.
The Go compiler does not yet use
loop invariants to eliminate bounds checks, but it does eliminate
bounds checks in the implicit indexing done by a range loop.
for i, pi := range p {
if i == len(m) {
break
}
if pi == 0 {
continue
}
// p -= k·g
q := p[i+1:]
exp := f.exp[f.log[pi]:]
for j, lg := range lgen {
if lg != 255 {
q[j] ^= exp[lg]
}
}
}
The code is in context in gf256.go.
Summary
We started with single bits 0 and 1. From those we constructed 8-bit polynomials—the elements of GF(28)—with overflow-free, easy-to-implement mathematical operations. From there we moved on to Reed-Solomon coding, which constructs its own polynomials built using elements of GF(28) as coefficients. That is, each Reed-Solomon message is interpreted as a polynomial, and each coefficient in that polynomial is itself a smaller polynomial.
Now that we know how to create Reed-Solomon encodings, the next post will look at some fun we can have with them.
April 05, 2012
Command Center

The byte order fallacy
i = (data[0]<<0) | (data[1]<<8) | (data[2]<<16) | (data[3]<<24);
i = (data[3]<<0) | (data[2]<<8) | (data[1]<<16) | (data[0]<<24);
i = *((int*)data);#ifdef BIG_ENDIAN/* swap the bytes */i = ((i&0xFF)<<24) | (((i>>8)&0xFF)<<16) | (((i>>16)&0xFF)<<8) | (((i>>24)&0xFF)<<0);#endif
- It's more code.
- It assumes integers are addressable at any byte offset; on some machines that's not true.
- It depends on integers being 32 bits long, or requires more #ifdefs to pick a 32-bit integer type.
- It may be a little faster on little-endian machines, but not much, and it's slower on big-endian machines.
- If you're using a little-endian machine when you write this, there's no way to test the big-endian code.
- It swaps the bytes, a sure sign of trouble (see below).
- Is shorter.
- Does not depend on alignment issues.
- Computes a 32-bit integer value regardless of the local size of integers.
- Is equally fast regardless of local endianness, and fast enough (especially on modern processsors) anyway.
- Runs the same code on all computers: I can state with confidence that if it works on a little-endian machine it will work on a big-endian machine.
- Never "byte swaps".
Stanley Lieber
(Untitled)
stanleylieber posted a photo:
(Untitled)
stanleylieber posted a photo:
(Untitled)
stanleylieber posted a photo:
(Untitled)
stanleylieber posted a photo:
April 01, 2012
research!rsc

Random Hash Functions
A hash function for a particular hash table should always be deterministic, right? At least, that's what I thought until a few weeks ago, when I was able to fix a performance problem by calling rand inside a hash function.
A hash table is only as good as its hash function, which ideally satisfies two properties for any key pair k1, k2:
- If k1 == k2, hash(k1) == hash(k2).
- If k1 != k2, it should be likely that hash(k1) != hash(k2).
Normally, following rule 1 would prohibit the use of random bits while computing the hash, because if you pass in the same key again, you'd use different random bits and get a different hash value. That's why the fact that I got to call rand in a hash function is so surprising.
If the hash function violates rule 1, your hash table just breaks: you can't find things you put in, because you are looking in the wrong places. If the hash function satisfies rule 1 but violates rule 2 (for example, “return 42”), the hash table will be slow due to the large number of hash collisions. You'll still be able to find the things you put in, but you might as well be using a list.
The phrasing of rule 1 is very important. It is not sufficient to say simply “hash(k1) == hash(k1)”, because that does not take into account the definition of equality of keys. If you are building a hash table with case-insensitive, case-preserving string keys, then “HELLO” and “hello” need to hash to the same value. In fact, “hash(k1) == hash(k1)” is not even strictly necessary. How could it not be necessary? By reversing rule 1, hash(k1) and hash(k1) can be unequal if k1 != k1, that is, if k1 does not equal itself.
How can that happen? It happens if k1 is the floating-point value NaN (not-a-number), which by convention is not equal to anything, not even itself.
Okay, but why bother? Well, remember rule 2. Since NaN != NaN, it should be likely that hash(NaN) != hash(NaN), or else the hash table will have bad performance. This is very strange: the same input is hashed twice, and we're supposed to (at least be likely to) return different hash values. Since the inputs are identical, we need a source of external entropy, like rand.
What if you don't? You get hash tables that don't perform very well if someone can manage to trick you into storing things under NaN repeatedly:
$ cat nan.py
#!/usr/bin/python
import timeit
def build(n):
m = {}
for i in range(n):
m[float("nan")] = 1
n = 1
for i in range(20):
print "%6d %10.6f" % (n, timeit.timeit('build('+str(n)+')',
'from __main__ import build', number=1))
n *= 2
$ python nan.py
1 0.000006
2 0.000004
4 0.000004
8 0.000008
16 0.000011
32 0.000028
64 0.000072
128 0.000239
256 0.000840
512 0.003339
1024 0.012612
2048 0.050331
4096 0.200965
8192 1.032596
16384 4.657481
32768 22.758963
65536 91.899054
$
The behavior here is quadratic: double the input size and the run time quadruples. You can run the equivalent Go program on the Go playground. It has the NaN fix and runs in linear time. (On the playground, wall time stands still, but you can see that it's executing in far less than 100s of seconds. Run it locally for actual timing.)
Now, you could argue that putting a NaN in a hash table is a dumb idea, and also that treating NaN != NaN in a hash table is also a dumb idea, and you'd be right on both counts.
But the alternatives are worse:
- If you define that NaN is equal to itself during hash key comparisons, now you have a second parallel definition of equality, to handle NaNs inside structs and so on, only used for map lookups. Languages typically have too many equality operators anyway; introducing a new one for this special case seems unwise.
- If you define that NaN cannot appear as a hash table key, then you have a similar problem: you need to build up logic to test for invalid keys such as NaNs inside structs or arrays, and then you have to deal with the fact that your hash table might return an error or throw an exception when inserting values under certain keys.
The most consistent thing to do is to accept the implications of NaN != NaN: m[NaN] = 1 always creates a new hash table element (since the key is unequal to any existing entry), reading m[NaN] never finds any data (same reason), and iterating over the hash table yields each of the inserted NaN entries.
Behaviors surrounding NaN are always surprising, but if NaN != NaN elsewhere, the least surprising thing you can do is make your hash tables respect that. To do that well, it needs to be likely that hash(NaN) != hash(NaN). And you probably already have a custom floating-point hash function so that +0 and −0 are treated as the same value. Go ahead, call rand for NaN.
(Note: this is different from the hash table performance problem that was circulating in December 2011. In that case, the predictability of collisions on ordinary data was solved by making each different table use a randomly chosen hash function; there's no randomness inside the function itself.)
March 20, 2012
Stanley Lieber
(Untitled)
stanleylieber posted a photo:
(Untitled)
stanleylieber posted a photo:
(Untitled)
stanleylieber posted a photo:
March 14, 2012
March 13, 2012
March 08, 2012
March 01, 2012
February 26, 2012
February 22, 2012
February 13, 2012
February 08, 2012
February 07, 2012
research!rsc

go blog()
Let my start by apologizing for the noisy duplicate posts. I know that people using RSS software to read this blog got a whole bunch of old posts shown as new yesterday, and the same thing happened again just now. I made some mistakes while moving the blog from one platform to another, which caused the first burp, and then I had to fix the mistakes, which caused the second burp. But it's done, and there won't be another batch of duplicates waiting for you tomorrow.
I've moved this blog off of Blogger onto App Engine, running on a custom app written in Go. The down side is that I had to implement functionality that Blogger used to handle for me, like generating the RSS feed, and that's both extra work and a chance to make mistakes, which I took full advantage of. The up side, however, is that it makes it significantly easier for me to automate the writing and publishing of posts, and to create posts with a computational aspect to the content. I'll be blogging in the coming months about both the new setup, which has some interesting technical aspects behind it (I can edit live posts in a real text editor, for one thing), and about other topics that can make use of the computation.
For now, though, it's just the same content on a new server. Enjoy.
February 05, 2012
January 31, 2012
January 21, 2012
January 20, 2012
January 19, 2012
research!rsc

Regular Expression Article #4
In January 2007 I posted an article on my web site titled “Regular Expression Matching Can Be Simple And Fast.” I intended this to be the first of three; the second would explain how to do submatching using automata, and the third would explain how to make a really fast DFA. These were inspired by my work on Google Code Search.
Today, the fourth article in my three-part series is available, accompanied by source code (as usual). This one describes how Code Search worked.
January 15, 2012
January 13, 2012
January 03, 2012
Stanley Lieber
seq
stanleylieber posted a photo:
January 01, 2012
Command Center

Esmerelda's Imagination
December 22, 2011
December 17, 2011
December 15, 2011
December 13, 2011
December 12, 2011
December 10, 2011
December 08, 2011
December 03, 2011
December 01, 2011
November 28, 2011
November 27, 2011
November 26, 2011
Stanley Lieber
nvidia geforce 8400gs 1680x1050x32 (fixed)
stanleylieber posted a photo:
code.google.com/p/plan9front/source/detail?r=18198808ffaa...
thanks, cinap!
nvidia geforce 8400gs 1680x1050x32
stanleylieber posted a photo:
November 24, 2011
November 13, 2011
November 11, 2011
Stanley Lieber
nvidia geforce 8400gs @ 1920x1080x32
stanleylieber posted a photo:
nvidia geforce 8400gs @ 1920x1080x8
stanleylieber posted a photo:
nvidia geforce @ 1920x1080x32
stanleylieber posted a photo:
November 10, 2011
November 09, 2011
November 06, 2011
Stanley Lieber
(Untitled)
stanleylieber posted a photo:
(Untitled)
stanleylieber posted a photo:
(Untitled)
stanleylieber posted a photo:
bcm
stanleylieber posted a photo:
November 02, 2011
October 22, 2011
newsham
Mu, Recursive types, functor composition...
If this all looks a bit like mental masturbation, it probably is, but it was quite enjoyable. If you're not into Haskell and functional programming you probably want to skip this.
{-# OPTIONS_GHC -XTypeOperators #-}
{- Recursive types in haskell. -}
module Main where
import Prelude hiding ( Maybe, Just, Nothing, maybe, sum, succ, map )
---- Pairs
data Pair a b = Pair a b
pair :: (a -> b -> c) -> Pair a b -> c
pair f (Pair a b) = f a b
instance Functor (Pair a) where
fmap f (Pair a b) = Pair a (f b)
---- Optional type
data Maybe a = Nothing | Just a
maybe :: c -> (a -> c) -> Maybe a -> c
maybe f _ Nothing = f
maybe _ g (Just x) = g x
instance Functor Maybe where
fmap f = maybe Nothing (Just . f)
---- Recursive types
newtype Mu a = In { mu :: (a (Mu a)) }
cata :: Functor f => (f a -> a) -> Mu f -> a
cata f = f . fmap (cata f) . mu
---- recursive peano numbers
--type Peano = Mu Maybe
zero = In $ Nothing
succ n = In $ Just n
mkNat 0 = In $ Nothing
mkNat n | n == 0 = zero
| n > 0 = succ $ mkNat (n - 1)
| n < 0 = error "bad natural"
unNat = cata $ maybe 0 (+ 1)
add x = cata $ maybe x succ
mul x = cata $ maybe zero $ add x
---- Composition of functors
newtype (g :. f) a = O { unO :: g (f a) }
instance (Functor f, Functor g) => Functor (g :. f) where
fmap f (O x) = O . (fmap . fmap) f $ x
---- proto recursive lists
type ListX a = Maybe :. Pair a
listx :: c -> (a -> b -> c) -> ListX a b -> c
listx f g = maybe f (pair g) . unO
---- recursive lists (ie. of ints)
--type ListI = Mu (ListX Int)
nil = In . O $ Nothing
cons x xs = In . O . Just $ Pair x xs
mkList [] = nil
mkList (x:xs) = cons x $ mkList xs
unList = cata $ listx [] (:)
sum = cata $ listx 0 (+)
map f = cata $ listx [] (\a b -> f a : b)
---- test it out...
main = do
let p m x = putStrLn (m ++ ": " ++ show x)
--
p "nat" $ unNat $ mkNat 5
p "add" $ unNat $ add (mkNat 5) (mkNat 3)
p "mul" $ unNat $ mul (mkNat 5) (mkNat 3)
--
p "list" $ unList $ mkList [1,2,3,4,5]
p "sum" $ sum $ mkList [1,2,3,4,5]
p "map" $ map (*2) $ mkList [1,2,3,4,5]
by newsham (noreply@blogger.com) at October 22, 2011 09:39 AM
October 21, 2011
October 11, 2011
October 09, 2011
October 06, 2011
newsham
Code Safety and Correctness II
Halfway There
We'll start by looking at a C implementation of memcpy written in a functional style:
void memcpy(char *p, char *q, int n)
{
if(n > 0) {
p[0] = q[0];
memcpy(p+1, q+1, n-1);
}
}
This is very non-idiomatic C code and for practical reasons we'd probably never write the function this way. If translated directly to assembly this code will execute much more slowly than the version we looked at last time. However, with certain optimizations it can actually execute just as quickly.
What makes this code different than our last implementation? The major difference is there are almost no state changes to track during execution. The parameters p, q and n that are passed in retain their value throughout the function. There is no difference between p at the end and p_arg (as we called it last time) at the start. In pure functional programming there is no difference between assignment and equality; since values never change, once a value is assigned to a variable, that value is equal to that value throughout its scope. This greatly eases the analysis.
We're not all the way there yet, though. This implementation of memcpy is still imperative as there is a state change when p[0] is set to q[0]. As a result each call to memcpy causes a state change and in fact that was the whole point. Memcpy is a primitive for changing the state of mutable arrays and is inherently imperative.
Our analysis will still make use of Hoare Logic. We start with the same precondition as we used last time:
// alloc(p[0..n]), init(q[0..n]), n >= 0
1: void memcpy(char *p, char *q, int n)
2: {
// alloc(p[0..n]), init(q[0..n]), n >= 0
3: if(n > 0) {
// alloc(p[0..n]), init(q[0..n]), n > 0
4: p[0] = q[0]; // safe
5: memcpy(p+1, q+1, n-1);
6: } else {
7: }
8: }
By propagating the precondition we can immediately see that the read of q[0] and the write of p[0] are safe. We would like to show that after the function completes all of p[0..n] equals q[0..n]. Let's assume this and see if we can verify it:
// alloc(p[0..n]), init(q[0..n]), n >= 0
1: void memcpy(char *p, char *q, int n)
2: {
// alloc(p[0..n]), init(q[0..n]), n >= 0
3: if(n > 0) {
// alloc(p[0..n]), init(q[0..n]), n > 0
4: p[0] = q[0];
// p[0] = q[0], init(p[0]),
// alloc(p[0..n]), init(q[0..n]), n > 0
5: memcpy(p+1, q+1, n-1);
6: } else {
// n = 0, p[0..n] = q[0..n]
7: }
// p[0..n] = q[0..n]?
8: }
The desired postcondition is trivially true in the else clause when n is zero (since [0..n] is empty). The only step remaining is to show that the desired postcondition is true at the end of the then clause. At line 5 we've met the precondition for calling memcpy. This is made more obvious if we rewrite the precondition to line 5. Therefore we can use our assumed postcondition after the call at line 5. This is induction.
// alloc(p[0..n]), init(q[0..n]), n >= 0
1: void memcpy(char *p, char *q, int n)
2: {
// alloc(p[0..n]), init(q[0..n]), n >= 0
3: if(n > 0) {
// alloc(p[0..n]), init(q[0..n]), n > 0
4: p[0] = q[0];
// p[0] = q[0], init(p[0]),
// alloc((p+1)[0..n-1]), init((q+1)[0..n-1]),
// (n-1) >= 0
5: memcpy(p+1, q+1, n-1);
// p[0] = q[0], init(p[0]),
// p[1..n] = q[1..n], init(p[1..n])
6: } else {
// n = 0, init(p[0..n]), p[0..n] = q[0..n]
7: }
// init(p[0..n]), p[0..n] = q[0..n]
8: }
We have shown that our assumption is true. We can see that there can be no integer overflows of p or q except when n is zero by our earlier definitions of alloc and init. We can also see that there can be no integer underflows of n. We have shown the function to be both safe and correct.
Notice that this proof is quite a bit simpler than the proof we constructed last time. Since p, q and n do not change throughout, the proof can be summarized as:
// alloc(p[0..n]), init(q[0..n]), n >= 0
1: void memcpy(char *p, char *q, int n)
2: {
// alloc(p[0..n]), init(q[0..n]), n >= 0
3: if(n > 0) {
4: p[0] = q[0]; // safe since n > 0
5: memcpy(p+1, q+1, n-1); // precond met
// p[0] = q[0] and p[1..n] = q[1..n]
6: }
// init(p[0..n]), p[0..n] = q[0..n]
7: }
We should point out that this proof has the same shortcomings pointed out last time. Most importantly, p and q can be aliased together in which case q can be altered and the correctness argument invalidated.
What's Next?
By using a functional style we were able to greatly improve the ease of reasoning about our code. Unfortunately the code we wrote doesn't run very efficiently in C. The C language is not ideally suited for writing in a functional style as it does not have some optimizations needed to run recursive code efficiently. It is also missing some features that would promote the use of recursion instead of iteration. To fully explore the functional programming style we'd be better suited working in another language.Although we were able to simplify our proof by using some functional techniques, we still came against some of the same limitations. These problems arose because our program is still imperative and still mutates data (although in a more limited way than our previous program). We can take this further and write programs in a purely functional style by using immutable data types. This brings many advantages but also a few downsides. In the end there will always be some imperative actions going on in our program (they still have to execute on imperative CPUs!) but we can greatly limit the amount of imperative code we have to reason about.
by newsham (noreply@blogger.com) at October 06, 2011 08:54 PM
Safety, Correctness and Strncpy - a quick note
When it comes time to analyze a function like strncpy we face a problem. There are two ways in which strncpy can be used -- the first is as a safer variant of strcpy. The second is as a truncating variant of strcpy. These are really two different functions and ideally would be served by two different API functions. When analyzing a program that uses strncpy we have to determine which of these two cases was intended. Why? The preconditions for safe use of strncpy are the same in both situations, however the preconditions to guarantee correct behavior are different in each situation! When strncpy is used as a replacement for strcpy, it will only behave correctly when the source string fits in the destination buffer. When strncpy is used to truncate a string, this precondition is not necessary.
Why is this important? It becomes a lot harder to determine if uses of strncpy are correct. Consider a static code analyzer that encounters a strncpy call. It may not have the context required to determine if a call that may truncate its result is correct or not since it may not be able to infer the intent of the programmer. So while strncpy may have been handy to improve the safety of programs, it may actually make it harder to ensure a programs correctness.
Edit: By request here are two small examples. This first example shows a use of strncpy to copy a substring:
// find the last dot, copy everything up to the dot.
p = strrchr(name, '.');
if(p && idx < sizeof(namebuf) - 1) {
int idx = p - name;
strncpy(namebuf, name, idx);
namebuf[idx] = 0;
}
This second example shows strncpy being used as a safe replacement for strcpy:
strncpy(namebuf, name, sizeof namebuf-1);
namebuf[sizeof namebuf - 1] = 0;
by newsham (noreply@blogger.com) at October 06, 2011 07:38 PM
October 05, 2011
October 03, 2011
newsham
Code Safety and Correctness
The memcpy function
We'll discuss the safety and correctness of the memcpy function implemented with the following C code:
1: void memcpy(char *p, char *q, int n)
2: {
3: while(n--)
4: *p++ = *q++;
5: }
To be really concrete we would have to define exactly what the C language means and be mindful of some of the cases where the language may leave behavior undefined. To simplify matters we'll assume that the code is translated in a direct manner (ie. without optimization) on an "ILP32" machine; that is, a machine on which integers and pointers are both 32-bit values stored as 2's complement numbers. In our fictitious dialect of C there are no undefined behaviors. For example, if you add one to (char)127 you'll get the well defined (char)-128 according to the "normal" behavior you'd expect with a CPU implementing 2's complement numbers.
Now let's consider some fairly straightforward questions: Is this function "safe"? Is it "correct"? We can't answer these questions without defining what safety and correctness mean.
What operations are not safe? In this small piece of code there are several things that can go wrong. We're reading from memory through a pointer. The pointer could be invalid. It could be valid and point to some data that we didn't intend to read. It could point to a memory cell that has never been initialized with valid data. We're also writing to memory through a pointer. The pointer could point to invalid memory or to memory we did not intend to write. We're doing arithmetic on integers and pointers. We might expect these values to operate as integers when in fact they are represented as finite 32-bit values.
Some notation
We can introduce some notation to define what we mean by safe operations. We'll define overflow(e) to mean that the expression e has a different result when evaluated with a finite representation than the result if all values are treated as ideal integers. In our analysis we'll repeated be using genuine integers, not the finite representations provided by C. We'll treat the use of any values after an overflow occurs as an unsafe operation. (Note: if the programmer wishes to rely on an the behavior of finite arithmetic she can explicitly use modular arithmetic or mask off select bits, in which case the expression would evaluate to the same value when using finite or arbitrary sized integers).When considering buffers we would like to discuss a few properties of the memory cells occupied by the buffer. We'll use the notation [n..m] to denote the range of integers (again, using genuine integers, not finite 32-bit representations) from n to m-1. For example [3..6] will represent the numbers 3, 4 and 5 but not 6. The ranges [6..6] and [7..2] are both empty.
We'll use the notation alloc(p[n]) to denote that the memory storage at (p+n) has been allocated to the p buffer. We'll use the notation alloc(p[n..m]) to represent that alloc(p[x]) holds for all x in [n..m] and we'll use similar notation later for other properties over a range. For example, alloc(p[3..6]) means that p[3], p[4] and p[5]are all allocated to p. We'll also asume that values are allocated in such a way that elements never wrap-around the address space. Said differently, alloc(p[n]) implies that overflow(p+n) is false. We'll treat any writes to p[n] to be unsafe unless alloc(p[n]) is true.
We'll use the notation init(p[n]) to denote that the memory cell at p+n is allocated and has been filled with meaningful data. We'll treat any reads of p[n] to be unsafe unless init(p[n]) is true.
Given these definitions its quite clear that we cannot guarantee the safety of the memcpy function for all possible arguments (consider memcpy(NULL, "test", 1000)!). The only way we could declare this function safe is if we imposed additional restrictions on the function. A reasonable set of restrictions are: n >= 0, alloc(p[0..n]) and init(q[0..n]). These restrictions say that the bytes from the source buffer have been initialized and the bytes of the destination buffer have been allocated. Lets analyze the program to see if we can convince ourselves that memcpy is safe with these restrictions.
Safety
To analyze the function we're going to informally use Hoare Logic. In Hoare Logic we list what is known before each statement is executed (the precondition), the statement to be executed, and what can be inferred after the statement is executed (the postcondition). It will be a lot easier to write down our analysis if we expand our definition of memcpy with a single side effect per line:1: void memcpy(char *p, char *q, int n)
2: {
3: while(1) {
4: int oldn = n;
5: n--;
6: if(!oldn)
7: break;
8: char c = *q;
9: *p = c;
10: p++;
11: q++;
12: }
13: }
To start our analysis, we write down our restriction on the arguments as a precondition to the function. This will also be the precondition to the while statement, which is the first statement in the function:
{ n >= 0, alloc(p[0..n]), init(q[0..n]) }
1: void memcpy(char *p, char *q, int n)
2: {
{ n >= 0, alloc(p[0..n]), init(q[0..n]) }
3: while(1) {
4: int oldn = n;
5: n--;
6: if(!oldn)
7: break;
8: char c = *q;
9: *p = c;
10: p++;
11: q++;
12: }
13: }
The precondition to the first statement inside the while loop must agree with the precondition of the while statement itself as well as the postcondition of any statement that loops back to the start of the while loop.
To analyze the loop we usually look for some property that remains true throughout the loop. Such properties are called loop invariants. In this case it appears that the program increments p and q and decrements n in step so that p+n and q+n remain invariant (except for brief periods between the update of n, p and q). It also looks like the precondition of the loop might remain true throughout the loop. We know that the property holds during the first iteration, but it must also hold when control loops around for us to state it as a precondition to line 4. Let's assume this is the case for now and verify that it is indeed the case (marking our assumption with a question mark):
{ n >= 0, alloc(p[0..n]), init(q[0..n]) }
1: void memcpy(char *p, char *q, int n)
2: {
{ n >= 0, alloc(p[0..n]), init(q[0..n]) }
3: while(1) {
{ n >= 0, alloc(p[0..n]), init(q[0..n]) }?
4: int oldn = n;
5: n--;
6: if(!oldn)
7: break;
8: char c = *q;
9: *p = c;
10: p++;
11: q++;
12: }
13: }
Filling in the postcondition after introducing the oldn variable is pretty simple. The postcondition after decrementing n is a little more interesting; for example since alloc(p[0..n]) was true before decrementing n, alloc([0..n+1]) must be true after n is replaced with n-1:
{ n >= 0, alloc(p[0..n]), init(q[0..n]) }?
4: int oldn = n;
{ oldn >= 0, n >= 0,
alloc(p[0..n]), init(q[0..n]) }?
5: n--;
{ oldn >= 0, n >= -1,
alloc(p[0..n+1]), init(q[0..n+1]) }?
6: if(!oldn)
{ oldn == 0, n = -1,
alloc(p[0..n+1]), init(q[0..n+1]) }?
7: break;
We note that there is no overflow(n-1) at line 5 since n >= 0. The break is the only exit point for the loop so the postcondition of the whole loop will be the precondition from the break statement. Note that since n is fixed we can rewrite the precondition to line 7 as: n = -1, alloc(p[0..0]), init(q[0..0]) and since the range [0..0] is empty we can discard the alloc() and init() properties entirely.
Continuing our analysis, we note that after the if statement fails n cannot be -1:
7: break;
{ oldn != 0, n > -1,
alloc(p[0..n+1]), init(q[0..n+1]) }?
8: char c = *q;
{ oldn != 0, n > -1,
alloc(p[0..n+1]), init(q[0..n+1]) }?
9: *p = c;
{ oldn != 0, n > -1,
alloc(p[0..n+1]), init(q[0..n+1]) }?
10: p++;
{ oldn != 0, n > -1,
alloc(p[-1..n]), init(q[0..n+1]) }?
11: q++;
{ oldn != 0, n > -1,
alloc(p[-1..n]), init(q[-1..n]) }?
At line 8 we arrive at an access of q[0]. We can rule this access as safe since by init(q[0..n+1]) with n > -1. At line 9 a value is stored into q[0] which is safe by alloc(p[0..n+1])with n > -1. At lines 10 and 11 the increments of p and q will not overflow if n > 0 by alloc(p[-1..n]) and init(p[-1..n]). However, if n = 0 we cannot rule out an overflow! Any further access through p and q after this point could be invalid. If there were other accesses through p and q later in the program we might have to worry about this, but as we've already shown that the pointer accesses in lines 8 and 9 are valid, we do not need to be concerned.
Finally after lines 10 and 11 we reach the end of the loop with a postcondition: n > -1, alloc(p[-1..n]), init(q[-1..n]). We can rewrite this as: n >= 0, alloc(p[0..n]), init(q[0..n]) by recognizing that [0..n] is a subset of [-1..n]. This provides a precondition for the next iteration of the while loop and confirms our earlier assumption.
Our analysis is complete and we have:
{ n >= 0, alloc(p[0..n]), init(q[0..n]) }
1: void memcpy(char *p, char *q, int n)
2: {
{ n >= 0, alloc(p[0..n]), init(q[0..n]) }
3: while(1) {
{ n >= 0, alloc(p[0..n]), init(q[0..n]) }
4: int oldn = n;
{ oldn >= 0, n >= 0,
alloc(p[0..n]), init(q[0..n]) }
5: n--; // no overflow(n-1) by n >=0
{ oldn >= 0, n >= -1,
alloc(p[0..n+1]), init(q[0..n+1]) }
6: if(!oldn)
{ oldn == 0, n == -1 }
7: break;
{ oldn != 0, n > -1,
alloc(p[0..n+1]), init(q[0..n+1]) }
8: char c = *q; // read q[0] valid by
// init(q[0..n+1]) and n >= 0
{ oldn != 0, n > -1,
alloc(p[0..n+1]), init(q[0..n+1]) }
9: *p = c; // write p[0] valid by
// alloc(p[0..n+1]) and n >= 0
{ oldn != 0, n > -1,
alloc(p[0..n+1]), init(q[0..n+1]) }
10: p++; // can overflow(p+1) of n == 0!
{ oldn != 0, n > -1,
alloc(p[-1..n]), init(q[0..n+1]) }
11: q++; // can overflow(q+1) if n == 0!
{ n >= 0, alloc(p[0..n]), init(q[0..n]) }
12: }
{ n == -1 }
13: }
One important safety property we did not yet discuss is termination; if we call memcpy will it ever return? Its not hard to convince ourselves that it will. If we start with n >= 0 and the while loop runs until n = 0 and decrements n once per iteration then eventually n will become zero and the loop will terminate.
Correctness
We've shown that given appropriate restrictions, memcpy can be shown to be safe. This does not mean that the function is correct. To determine if it is correct we first have to come up with a definition of what correct behavior is. A reasonable choice is to say that after memcpy(d, s, m) is called all of d[x] equal s[x] for x in [0..n]. Let's see if we can derive this as a postcondition of memcpy using Hoare Logic.In our function the value of the arguments p, q and n are altered throughout the function. This is problematic since we want to say something about the original values of these arguments in the postcondition. To deal with this, we'll introduce the notation p_arg to denote the original value of the p argument, with similar notation for q and n. Next we'll define d = p - p_arg which is how far p has moved past p_arg (and how far q has moved past q_arg) while executing memcpy. This will allow us to relate the final value of p (and q) with the initial value. We note that d + n remains invariant with the value n_arg.
With these observations in mind we note that at any point in the execution, p[-d..0] has been set to values from q[-d..0]. The details of the analysis are:
{ n >= 0, alloc(p[0..n]), init(q[0..n]) }
1: void memcpy(char *p, char *q, int n)
2: {
{ d = 0, d+n = n_arg, n >= 0,
init(p[0..0]), p[0..0] = q[0..0] }
3: while(1) {
{ d+n=n_arg, n >= 0,
init(p[-d..0]), p[-d..0] = q[-d..0] }
4: int oldn = n;
{ d+n=n_arg, oldn >= 0, n >= 0,
init(p[-d..0]), p[-d..0] = q[-d..0] }
5: n--;
{ d+n+1 = n_arg, oldn >= 0, n >= -1,
init(p[-d..0]), p[-d..0] = q[-d..0] }
6: if(!oldn)
{ oldn = 0, n = -1, d=n_arg,
init(p[-d..0]), p[-d..0] = q[-d..0] }
7: break;
{ d+n+1 = n_arg, oldn != 0, n > -1,
init(p[-d..0]), p[-d..0] = q[-d..0] }
8: char c = *q;
{ d+n+1 = n_arg, n >= 0,
init(p[-d..0]), p[-d..0] = q[-d..0] }
9: *p = c; // now p[0] = q[0]
{ d+n+1 = n_arg, n >= 0,
init(p[-d..1], p[-d..1] = q[-d..1] }
10: p++; // now d is one larger
{ d+n = n_arg, n >=0,
init(p[-d..0], p[-d..0] = q[-d+1..1] }
11: q++;
{ d+n = n_arg, n >= 0,
init(p[-d..0]), p[-d..0] = q[-d..0] }
12: }
{ n = -1, init(p[-n_arg..0],
p[-n_arg..0] = q[-n_arg..0] }
13: }
(Note: to simplify the analysis slightly and limit the amount of information we write down in the pre- and postconditions we skipped over the analysis that d is (almost always) q - q_arg. Finally at the end of the procedure we can use our definition of d to rewrite our postcondition as init(p_arg[0..n_arg]), p_arg[0..n_arg] = q_arg[0..n_arg] proving the correctness of the memcpy function.
Can't we simplify?
// precond: alloc(p[0..n]), init(q[0..n]), n >= 0
1: void memcpy(char *p, char *q, int n)
2: {
// invariant: alloc(p[-d..n']), init(q[-d..n']),
// p[-d..0] = q[-d..0], n' >= 0
// where n' is n before the postdecrement
// and d = p-p_arg, d = q-q_arg.
3: while(n--) {
// n' > 0
4: *p++ = *q++;
5: }
// d = n_arg, p[-d..0] = q[-d..]
// so p_arg[0..n_arg] = q_arg[0..n]
6: }What's a proof worth?
We've shown that memcpy is both safe and correct if called correctly. You might be surprised to learn that there are some conditions where calling memcpy with "correct" arguments can lead to incorrect or unsafe behavior! What exactly is our proof worth?Consider what happens if you call memcpy with two buffers that overlap. Let's say we have a buffer p that holds "TESTING 1 2 3" and q that points to the fourth byte of p. What happens if we call memcpy(p, q, 8)? After the call p will contain "ING 1 2 1 2 3". In this case nothing "bad" happened, but p[0..8] is most definitely not equal to q[0..8]! During execution each p[x] was set to each q[x] for x in [0..8] but some of the values of q were altered in the process. Somehow in our analysis we had assumed that the values of q[0..8] would remain constant and they did not. We've encountered something called aliasing. Some of the values of p[x] were aliased to some values of q which resulted in q being altered outside of our analysis. Another precondition that must hold for our definition of correctness to hold must be that p and q are not aliased to each other.
Are there other ways in which q could have been altered while memcpy executes? Definitely! If our program is multi-threaded then another thread could have altered parts of p or q or even worse the state used by memcpy during execution! Even more extremely, our program could be altered during execution by someone using a debugger, or using other OS mechanisms to manipulate the program. Such manipulation could clearly violate our analysis. There could also be bugs in the compiler that translated our C program to assembly, the operating system that runs the program or in the implementation of the CPU. Hardware failures could result in the program crashing entirely or failing more subtly with the corruption of the buffers or internal state of memcpy. In short, there are still a wide number of things that can go wrong to violate the assumptions of our proof! Its important that we try to understand the limitations of our analysis.
Try your own
Consider what happens if the arguments to strcpy are aliased. Why is the behavior so different than in the memcpy case?
What Next?
We did some analysis of imperative code using Hoare Logic in this article. Most programmers already think about the kinds of issues we encountered when they write or analyze programs. Having notation and tools like Hoare Logic allow us to communicate these ideas efficiently to others or write them down and manipulate them in small, less-error-prone steps so that we can work on more difficult problems than we can easily solve in our head. Writing down our work can also provide another benefit -- it slows us down and focuses our attention on important safety issues. This is especially helpful when using dangerous constructs (like pointer manipulation) in safety critical code (such as inside an operating system kernel).Unfortunately there is no room for our analysis in our C programs themselves. We can state restrictions in comments or in documentation and we might even be able to add some asserts to check some of the properties, but unfortunately the C language does not understand or validate any of our analysis. Ideally all preconditions would be provided as additional arguments to a function and the postcondition would be part of the return value or return type of a function or operation. This would require we work in a language that supported representing and manipulating proofs and would probably burden the programmer with filling in the details of the analysis. However, without the compiler checking over our work, we are bound to make mistakes.
Analysis of imperative programs can be a little awkward as the program state mutates. At times we want to discuss the particular value of a variable in a pre- or postcondition after it has been mutated (as we did with p_arg for example). Another style of programming, functional programming, can be manipulated mathematically more naturally. Next time we'll go through a small example in a (mostly) functional programming language.
by newsham (noreply@blogger.com) at October 03, 2011 08:40 PM
October 02, 2011
September 30, 2011
September 24, 2011
newsham
Simple instrumenation in Qemu
Qemu is a free and open source system emulator. It works by performing dynamic translation of the code it is running from the instruction set being execute (in my case i386) to whatever instruction set your computer runs natively. The translation is performed "Just In Time" on individual blocks of code whenever new code is encountered that hasn't been translated yet. In this case we're going to treat Qemu as if it was a computer with a customizable CPU -- one we could easily repurpose to perform something a real cpu doesn't normally do. It turns out that customizing Qemu can be quite simple.
Qemu already has a logging facility that can be used to show what code is being translated, what intermediate operations are emitted, what target instructions are emitted, what blocks are being executed, etc. You can use these options from the command line by specifying "-D logfile -d list,of,flags" or from the qemu console with the commands "logfile filename" and "log list,of,flags". In the following figure you can see a list of the flag options:
Our first step is to add a new flag called "extras" which we will use to turn on and off any new tracing features we add:
Next we take a look at the current translation of dynamic calls and the code that generates it, so we can figure out where to add our patch. This is as simple as running with "-d in_asm,op" and looking at the resulting log file:
Here we see an instruction we're interested in at 0xf332d. The code is translated into an intermediate format called TCG. This format is documented in qemu/tcg/README. Here we see that the address of ebx (which is a variable representing the virtual EBX register) is loaded into the tmp2 register and then dereferenced to load it's value into tmp0. The remaining instructions emulate pushing the program counter onto the stack before updating the new program counter which is dereferenced off of the "env" variable. Below we see the code in qemu/target-i386/translate.c that generated this code:
You can find the details of the call instruction in the IA-32 Intel Architecture Software Developer's Manual Volume 2: Instruction Set Reference. The code right before the switch statement handles loading of the target address into the temp0 register for several different variants of the opcode. The code in the switch statement then generates the code that simulates the stack push of the return address and the setting of the new program counter.
What we would like to do is to call a logging function every time an indirect call is executed. This function would log the current program counter and the target address. This is fairly straightforward since the target address has already been computed into the temp0 address. First we define a new helper function in helper.h. This will define a "gen_helper_tracecall" function which will generate a call to our helper. All that is left then is to call our helper at the top of the switch statement with the target value from temp0 and the current program counter, and define our helper function. The helper function simply writes to the log if the "extras" logging flag has been set:
Thats it! Now if we run qemu with the "-D calls.txt -d extras" flags, we get a log of all of the dynamic call targets in the "calls.txt" file. Or we could run qemu, switch to the console and turn on tracing with "log extras" and turn it off again with "log none".
So that was pretty simple and it runs fairly quickly. This is a really powerful technique and we can get a lot of mileage out of it, but it would be good to have more control. There are a lot of things we can do going forward to make this more powerful. One thing that comes to mind is adding (operating system specific) hooks that track what process or thread is currently running to allow filtering of events by process and thread. It would also be useful to keep an internal log of unique targets and only emit targets that haven't yet been logged.
by newsham (noreply@blogger.com) at September 24, 2011 11:49 PM
September 19, 2011
September 18, 2011
Command Center

User experience
NineTimes - Inferno and Plan 9 News
Inferno for Android phones!
John Floren announced on 9fans that himself and some of the folks at Sandia National Labs have inferno running on a few android devices.
We would like to announce the availability of Inferno for Android phones. Because our slogan is "If it ain't broke, break it", we decided to replace the Java stack on Android phones with Inferno. We've dubbed it the Hellaphone--it was originally Hellphone, to keep with the Inferno theme, but then we realized we're in Northern California and the change was obvious.
The Hellaphone runs Inferno directly on top of the basic Linux layer provided by Android. We do not even allow the Java system to start. Instead, emu draws directly to the Linux framebuffer (thanks, Andrey, for the initial code!) and treats the touchscreen like a one-button mouse. Because the Java environment doesn't start, it only takes about 10 seconds to go from power off to a fully-booted Inferno environment.
As of today, we have Inferno running on the Nexus S and the Nook Color. It should also run on the Android emulator, but we haven't tested that in a long time. The cell radio is supported, at least on the Nexus S (the only actual phone we've had), so you can make phone calls, send texts, and use the data network.
A video John made showing what's working so far.
Great job guys!
6th International Workshop on Plan 9
This years iwp9 is going to be held at Universidad Rey Juan Carlos in Fuenlabrada, Madrid, Spain. The workshop is taking place October 20 — 21, 2011. The registration deadline (which is subject to change) is on October 10th.
More information at iwp9.org.
September 15, 2011
September 12, 2011
September 02, 2011
August 23, 2011
Command Center

Regular expressions in lexing and parsing
parsing. Regular expressions are hard to write, hard to write well,
and can be expensive relative to other technologies. (Even when they
are implemented correctly in N*M time, they have significant
overheads, especially if they must capture the output.)
Lexers, on the other hand, are fairly easy to write correctly (if not
as compactly), and very easy to test. Consider finding alphanumeric
identifiers. It's not too hard to write the regexp (something like
"[a-ZA-Z_][a-ZA-Z_0-9]*"), but really not much harder to write as a
simple loop. The performance of the loop, though, will be much higher
and will involve much less code under the covers. A regular expression
library is a big thing. Using one to parse identifiers is like using a
Ferrari to go to the store for milk.
And when we want to adjust our lexer to admit other character types,
such as Unicode identifiers, and handle normalization, and so on, the
hand-written loop can cope easily but the regexp approach will break
down.
A similar argument applies to parsing. Using regular expressions to
explore the parse state to find the way forward is expensive,
overkill, and error-prone. Standard lexing and parsing techniques are
so easy to write, so general, and so adaptable there's no reason to
use regular expressions. They also result in much faster, safer, and
compact implementations.
statically-defined patterns, but regular expressions' strength is that
they provide a way to express patterns dynamically. They're great in
text editors and search tools, but when you know at compile time what
all the things are you're looking for, regular expressions bring far
more generality and flexibility than you need.
Finally, on the point about writing well. Regular expressions are, in
my experience, widely misunderstood and abused. When I do code reviews
involving regular expressions, I fix up a far higher fraction of the
regular expressions in the code than I do regular statements. This is
a sign of misuse: most programmers (no finger pointing here, just
observing a generality) simply don't know what they are or how to use
them correctly.
Encouraging regular expressions as a panacea for all text processing
problems is not only lazy and poor engineering, it also reinforces
their use by people who shouldn't be using them at all.
So don't write lexers and parsers with regular expressions as the
starting point. Your code will be faster, cleaner, and much easier to
understand and to maintain.
August 13, 2011
July 26, 2011
Software Magpie

My latest squeeze
root@squeeze1's password:This network device is for authorized use only. Unauthorized or improper useof this system may result in you hearing very bad music. If you do not consentto these terms, LOG OFF IMMEDIATELY.Ha, only joking. Now you have logged in feel free to change your root passwordusing the 'passwd' command. You can safely modify any of the files on thissystem. A factory reset (press and hold add on power on) will remove all yourmodifications and revert to the installed firmware.Enjoy!
July 20, 2011
July 17, 2011
NineTimes - Inferno and Plan 9 News
Plan 9 from the People's Front of cat-v.org (9front)
Plan 9 has been forked to start a development out of the Bell‐Labs (or whatever they are called these days…). This true community‐approach allows further development of Plan 9, even if the shrinking resources at Bell‐Labs for Plan 9 are vanishing.
The homepage and the code can be both found at Google code. You can boot 9front from the regulary built live cd or build the binaries in your existing Plan 9 installation. Installation instructions and further information can be obtained at the 9front wiki.
Everyone is invited to join the development of 9front. Discussions about 9front are held in #cat‐v on irc.freenode.net.
July 03, 2011
catena
Credo example: from lex and c source to cygwin executable, across directories
This article walks through building a trivial example of lex source
code into C, and then compiling the generated C source code into
object files and an executable in a different directory. The point is
to demonstrate using dodep to generate and customize build scripts
and list dependencies, and credo to execute the build process.
Lines which start with ; are shell commands; lines without are output.
Key commands are displayed in red text.
Starting state
We start with the files lorem, src/dcr.l, src/header.c, src/lex.h,
and an empty obj directory. Each line of lorem ends with a
carriage return (not usually printed), which we want to strip.
header.c is an ordinary C source file to compile and link.
lex.h gives us a local header to look for.
Generate source code
; cd src
; echo flex > dcr.c.lex.env
We first go into the src directory, and set the lex shell variable to flex,
to specify which lexer to use. To demonstrate an unusual feature,
that would be valid across ports to different operating systems,¹
we’ll capture it with this command.
¹ Inferno and Plan 9 store variables by name in the directory /env,
different for each process. This gives it a definite advantage in
capturing dependencies on variables, since we can just list the name
of the shell-variable file as a dependency.
src/dcr.c.lex.env:1: flex
This setting applies (is transformed into a shell variable) when credo
processes the target dcr.c, if dcr.c depends on /env/lex.
; dodep (c lex l c) dcr.c
credo dcr.c
We ask dodep to generate a shell script and list of dependencies with
this command. The content of these files comes from a library,
indexed by the four parameters given before the name of the file we
want to build. In this case, we want to look in the “c” namespace,
at the command “lex”, to translate an “l” file to a “c” file.
The generated dependency list includes the name of the lex source file,
and references to the variables lex and lflags.
src/dcr.c.dep:1: 0 dcr.l
src/dcr.c.dep:2: 0 /env/lex
src/dcr.c.dep:3: 0 /env/lflags
Credo passes the name of its target, the C source file, to the shell script,
which prints the name of the C source file if it was able to create it.
src/dcr.c.do:1: #!/dis/sh
src/dcr.c.do:2: c = $1
src/dcr.c.do:3: (sum l) = `{grep '\.l$' $c^.dep}
src/dcr.c.do:4:
src/dcr.c.do:5: if {no $lex} {lex = lex}
src/dcr.c.do:6:
src/dcr.c.do:7: if {
src/dcr.c.do:8: flag x +
src/dcr.c.do:9: os -T $lex $lflags $l
src/dcr.c.do:10: mv lex.yy.c $c
src/dcr.c.do:11: } {
src/dcr.c.do:12: echo $c
src/dcr.c.do:13: }
The hosted-Inferno command os calls host-OS commands. Under Cygwin,
it calls Cygwin or Windows commands.
Dodep finally prints a credo command to build the requested target.
; credo dcr.c
credo dcr.l
credo dcr.c
os -T flex dcr.l
mv lex.yy.c dcr.c
dcr.c
Credo builds all its non-/env dependencies in parallel. Once these
are complete, it determines whether the checksum of each file on which
it depends is different than the checksum stored for that file the
last time credo built this target.
This credo command creates a build-avoidance marker file dcr.l.redont,
which tells further runs of credo that the file dcr.l does not need
any processing, so exit early. It calls the host’s flex program,
on the path set when the Inferno environment started, to create the
target file dcr.c.
It updates the check sums in the file dcr.c.dep, to reflect content at
the time of compilation. This means that each target has its own view
of its dependencies, and any change to any file on which it depends,
or a change to the list of files on which it depends, prompts the
target to rebuild.
src/dcr.c.dep:1: 79f9925952d9cfb5a58270c0e2b67691 dcr.l
src/dcr.c.dep:2: 897a779351421523cadbafccdce22efe /env/lex
src/dcr.c.dep:3: 0 /env/lflags
It creates these checksum files to detect any changes to the target’s
dependencies or build script.
src/dcr.c.dep.sum:1: c33129421847b7d897d4e244caf1b8c0 dcr.c.dep
src/dcr.c.do.sum:1: 71d94d651922bd5ff5b543bba52f47d0 dcr.c.do
It also checksums the target file itself. If credo finds, the next
time it runs, that the current checksum of the target does not match,
then it assumes that the target was changed by hand, and will not
overwrite it.
src/dcr.c.sum:1: 2fed3667f390fd80993e090a7eb92c75 dcr.c
Compile objects and executable
We now have all the source, so we go to the object-file and executable
directory, and ask dodep to provide do and dep files to build dcr.exe.
From the “c”-language toolset, we use “cc” to compile an “o”bject file
into an “exe”cutable.
; cd ../obj
; dodep (c cc o exe) dcr.exe
credo dcr.exe
This time the dodep command created two *.do files, dcr.exe.dep.do and
dcr.exe.do, instead of a do and dep file for the target dcr.exe.
obj/dcr.exe.dep.do:1: #!/dis/sh
obj/dcr.exe.dep.do:2: dep = $1
obj/dcr.exe.dep.do:3: exe = `{echo $dep | sed 's,\.dep,,'}
obj/dcr.exe.dep.do:4: (stem ext o) = `{crext o $exe}
obj/dcr.exe.dep.do:5:
obj/dcr.exe.dep.do:6: adddep $exe /env/ars /env/cc /env/cflags /env/ldflags /env/objs
obj/dcr.exe.dep.do:7: adddep $exe $o
obj/dcr.exe.dep.do:8: adddep $exe `{/lib/do/c/coneed $o}
dcr.exe.dep.do creates the dependency list dcr.exe.dep for the target
dcr.exe by adding a set of credo-specific (ars and objs) and standard
(cc, cflags, and ldflags) shell variables; the primary object file,
named for the executable; and any other object files which the primary
one needs. The tool coneed does this last bit of analysis by compiling
the primary object file, looking for unresolved symbols in available
source code, compiling the source code to make sure, and printing the
set of matching object files.
obj/dcr.exe.do:1: #!/dis/sh
obj/dcr.exe.do:2: exe = $1
obj/dcr.exe.do:3: if {no $cc} {cc = cc}
obj/dcr.exe.do:4: if {
obj/dcr.exe.do:5: flag x +
obj/dcr.exe.do:6: os -T $cc $cflags -o $exe $objs $ars $ldflags
obj/dcr.exe.do:7: } {
obj/dcr.exe.do:8: echo os -T ./$exe
obj/dcr.exe.do:9: }
To gather enough information to compile the executable, credo relays
information from dependencies back to calling targets through *.relay
files, which are shell scripts that set the environment for calling targets.
Finally, to start the build process, we locate the source code,
record which compilation tools to use, and again call credo.
; srcdir = ../src/
; echo cpp-3 > default.cpp.env
; echo -I../src/ > default.cppflags.env
; echo gcc-3 > default.cc.env
; credo dcr.exe
credo dcr.exe.dep
os -T gcc-3 -I../src/ -c ../src/dcr.c
os -T gcc-3 -I../src/ -c ../src/header.c
credo dcr.o.dep
credo dcr.o
credo header.o.dep
credo header.o
credo dcr.exe
os -T gcc-3 -o dcr.exe dcr.o header.o
os -T ./dcr.exe
Credo first runs dcr.exe.dep.do to find and store the dependencies of
dcr.exe in dcr.exe.dep. dcr.exe.dep is an implicit dependency of dcr.exe,
so credo runs its *.do script automatically.
obj/dcr.exe.dep:1: 0 /env/ars
obj/dcr.exe.dep:2: 131eb9ab2f6a65b34e0158de1b321e3c /env/cc
obj/dcr.exe.dep:3: 0 /env/cflags
obj/dcr.exe.dep:4: 0 /env/ldflags
obj/dcr.exe.dep:5: 84a1a3c306e006dd723bebe9df29ee6c /env/objs
obj/dcr.exe.dep:6: 3f0d90c1c7483ad1805080cf9e48d050 dcr.o
obj/dcr.exe.dep:7: 1db618b791dc87ac0bd5504f69434273 header.o
Coneed uses $srcdir to find dcr.c, and the setting of cppflags in
default.cppflags.env to find lex.h. Once coneed compiles dcr.o,
it finds the unresolved symbol for the header function, finds a
definition of header() in header.c, and compiles header.o to verify
that it defines the symbol. Coneed finds no other unresolved symbols
supplied by other source code in $srcdir (c.f. printf), so it stops.
Coneed uses “dodep (c cc c o)” to compile the source code in $srcdir
into object files in the current directory (obj). This generates
*.o.dep.do and *.o.do for each source file: those for dcr are shown,
the ones for header are identical.
obj/dcr.o.dep.do:1: #!/dis/sh
obj/dcr.o.dep.do:2: dep = $1
obj/dcr.o.dep.do:3: o = `{echo $dep | sed 's,\.dep,,'}
obj/dcr.o.dep.do:4: (stem ext c) = `{crext c $srcdir^$o}
obj/dcr.o.dep.do:5:
obj/dcr.o.dep.do:6: adddep $o /env/cc /env/cflags /env/cppflags
obj/dcr.o.dep.do:7: adddep $o $c
obj/dcr.o.dep.do:8: adddep $o `{/lib/do/c/findh $c}
obj/dcr.o.do:1: #!/dis/sh
obj/dcr.o.do:2: o = $1
obj/dcr.o.do:3: (sum c) = `{grep '\.c$' $o^.dep}
obj/dcr.o.do:4:
obj/dcr.o.do:5: if {no $cc} {cc = cc}
obj/dcr.o.do:6:
obj/dcr.o.do:7: if {
obj/dcr.o.do:8: flag x +
obj/dcr.o.do:9: os -T $cc $cflags $cppflags -c $c
obj/dcr.o.do:10: } {
obj/dcr.o.do:11: echo 'objs = $objs '^$o > $o^.relay
obj/dcr.o.do:12: }
Before credo runs dcr.o.do it runs dcr.o.dep.do to generate dcr.o.dep
(header.o likewise). To find the paths to C header files it calls findh,
which gathers header-file #includes from the C source files,
and searches for them in local and system directories using cppflags
and the search list printed by $cpp -v.
obj/dcr.o.dep:1: 131eb9ab2f6a65b34e0158de1b321e3c /env/cc
obj/dcr.o.dep:2: 0 /env/cflags
obj/dcr.o.dep:3: 9134215aef7b4657beb5c4bb7a20d4a1 /env/cppflags
obj/dcr.o.dep:4: 2fed3667f390fd80993e090a7eb92c75 ../src/dcr.c
obj/dcr.o.dep:5: feea1fa232f248baa7a7d07743ee86c4 ../src/lex.h
obj/dcr.o.dep:6: fb584676de41ee148c938983b2338f5b /n/C/cygwin/usr/include/stdio.h
obj/dcr.o.dep:7: f6409b1008743b1866d4ad8e53f925cc /n/C/cygwin/usr/include/string.h
obj/dcr.o.dep:8: 468b1dd86fef03b044dceea020579940 /n/C/cygwin/usr/include/errno.h
obj/dcr.o.dep:9: 4e6678324ba6b69666eba8376069c950 /n/C/cygwin/usr/include/stdlib.h
obj/dcr.o.dep:10: c7575313e03e7c18f8c84a5e13c01118 /n/C/cygwin/usr/include/inttypes.h
obj/dcr.o.dep:11: a8fd5fa102b8f74d1b96c6c345f0e22d /n/C/cygwin/usr/include/unistd.h
obj/header.o.dep:1: 131eb9ab2f6a65b34e0158de1b321e3c /env/cc
obj/header.o.dep:2: 0 /env/cflags
obj/header.o.dep:3: 9134215aef7b4657beb5c4bb7a20d4a1 /env/cppflags
obj/header.o.dep:4: ecd87752a211e69078e6bc37afbb561b ../src/header.c
obj/header.o.dep:5: feea1fa232f248baa7a7d07743ee86c4 ../src/lex.h
obj/header.o.dep:6: fb584676de41ee148c938983b2338f5b /n/C/cygwin/usr/include/stdio.h
At this point credo has the dependencies for dcr.exe, so it works
through them, calling the *.relay files—generated by the object files’
do scripts—to gather object names in $objs.
obj/dcr.o.relay:1: objs = $objs dcr.o
obj/header.o.relay:1: objs = $objs header.o
There’s not much to do since coneed already compiled the object files,
so it links them, and prints an os command to run the executable,
since Inferno can’t directly run a Cygwin executable.
Clean up
To clean up, we remove generated files in the src and obj directories.
; rm -f *.redoing *.redont *.renew *.reold *.sum
This removes all the temporary state files created by credo.
Once this is done credo will rebuild from scratch, and reconstruct
each target’s view of its dependencies.
; rm -f `{lsdo | sed 's,^c?redo ,,'}
This removes all the targets created by do scripts. The lsdo command
(called by credo with no targets) prints credo commands for all the
credo targets in the current directory. For example:
; cd src; credo
credo dcr.c
; cd obj; credo
credo dcr.exe
credo dcr.exe.dep
credo dcr.o
credo dcr.o.dep
credo header.o
credo header.o.dep
Once the targets are removed, credo will unconditionally generate them.
; rm -f *.do *.dep *.relay
This removes all the instructions credo uses to build files.
These may usually be regenerated by dodep, adddep (which adds
to the given target’s dependency list the given files), and
rmdep (which removes the given files).
A single library script is provided to remove the state, target,
and dodep files.
; rm -f *.env
This removes default and per-target environment settings.
Once we remove these sets of files, the directories contain only the
files present in their starting state.
July 01, 2011
research!rsc

Floating Point to Decimal Conversion is Easy
Floating point to decimal conversions have a reputation for being difficult. At heart, they're really very simple and straightforward. To prove it, I'll explain a working implementation. It only formats positive numbers, but expanding it to negative numbers, zero, infinities and NaNs would be very easy.
An IEEE 64-bit binary floating point number is an integer v in the range [252, 253) times a power of two: f = v × 2e. Constraining the fractional part of the unpacked float64 to the range [252, 253) makes the representation unique. We could have used any range that spans a multiplicative factor of two, but that range is the first one in which all the values are integers.
In Go, math.Frexp unpacks a float64 into f = fr × 2exp where fr is in the range [½, 1). (C's frexp does too.) Converting to our integer representation is easy:
fr, exp := math.Frexp(f) v := int64(fr * (1<<53)) e := exp - 53
To convert the integer to decimal, we'll use strconv.Itoa64 out of laziness; you know how to write the direct code.
buf := make([]byte, 1000) n := copy(buf, strconv.Itoa64(v))
The allocation of buf reserves space for 1000 digits. In general 1/2e requires about 0.7e non-zero decimal digits to write in full. For a float64, the smallest positive number is 1/21074, so 1000 digits is plenty. The second line sets n to the number of bytes copied in from the string representation of the (integer) v. Throughout, n will be the number of digits in buf. Note that we're working with ASCII decimal digits '0' to '9', not bytes 0-9.
Now we've got the decimal for v stored in buf. Since f = v × 2e, all that remains is to multiply or divide buf by 2 the appropriate number of times (e or -e times).
Here's the loop to handle positive e:
for ; e > 0; e-- {
δ := 0
if buf[0] >= '5' {
δ = 1
}
x := byte(0)
for i := n-1; i >= 0; i-- {
x += 2*(buf[i] - '0')
x, buf[i+δ] = x/10, x%10 + '0'
}
if δ == 1 {
buf[0] = '1'
n++
}
}
dp := n
Each iteration of the inner loop overwrites buf with twice buf. To start, the code determines whether there will be a new digit (δ = 1), which happens when the leading digit is at least 5. Then it runs up the number from right to left, just as you learned in grade school, multiplying each digit by two and using x to carry the result. The digit buf[i] moves into buf[i+δ]. At the end, if the code needs to insert an extra digit, it does. Run e times.
After the loop finishes, we record in dp the current location of the decimal point. Since buf is still an integer (it started as an integer and we've only doubled things), the decimal point is just past all the digits.
Of course, e might have started out negative, in which case we've done nothing and still need to halve buf e times:
for ; e < 0; e++ {
if buf[n-1]%2 != 0 {
buf[n] = '0'
n++
}
δ, x := 0, byte(0)
if buf[0] < '2' {
δ, x = 1, buf[0] - '0'
n--
dp--
}
for i := 0; i < n; i++ {
x = x*10 + buf[i+δ] - '0'
buf[i], x = x/2 + '0', x%2
}
}
Dividing by two needs an extra digit if the last digit is odd, to store the final half; in that case we add a 0 to buf so that we'll have room to store a completely precise answer.
After adding the 0, we can set up for the division itself. If the first digit is less than 2, it's going to become a zero; in the interest of avoiding leading zeros we use an initial partial value x and move digits up (δ = 1) during the division. The multiplication ran from right to left copying from buf[i] to buf[i+δ]. The division runs left to right copying from buf[i+δ] to buf[i].
Now buf[0:n] has all the non-zero digits in the exact decimal representation of our f, and dp records where to put the decimal point. We could stop now, but we might as well implement correct rounding while we're here.
The interesting case is when we have more digits than requested (n > ndigit). To make the decision, just like in grade school, we look at the first digit being removed. If it's less than 5, we round down by truncating. If it's greater than 5, we round up by incrementing what's left after truncation. If it's equal to 5, we have to look at the rest of the digits being dropped. If any of the rest of the digits are nonzero, then rounding up is more accurate. Otherwise we're right on the line. In grade school I was taught to handle this case by rounding up: 0.5 rounds to 1. That's a simple rule to teach, but breaking this tie by rounding to the nearest even digit has better numerical properties, because it rounds up and down equally often, and it is the usual rule employed in real calculations.
This all results in the thunderclap rounding condition:
buf[prec] > '5' || buf[prec] == '5' && (nonzero(buf[prec+1:n]) || buf[prec-1]%2 == 1)
You can see why children are taught buf[prec] >= '5' instead.
Anyway, if we have to increment after the truncation, we're still working in decimal, so we have to handle carrying incremented 9s ourselves:
i := prec-1
for i >= 0 && buf[i] == '9' {
buf[i] = '0'
i--
}
if i >= 0 {
buf[i]++
} else {
buf[0] = '1'
dp++
}
The loop handles the 9s. The if increments what's left, or, if we turned the whole string into zeros, it simulates inserting a 1 at the beginning by changing the first digit to a 1 and moving the decimal place.
Having done that and set n = prec, we can piece together the actual number:
return fmt.Sprintf("%c.%se%+d", buf[0], buf[1:n], dp-1)
That prints the first digit, then a decimal point, then the rest of the digits, and finally the e±N suffix. The exponent must adjust the number by dp−1 because we are printing all but the first digit after the decimal point.
That's all there is to it. To print f = v × 2e you write v in decimal, multiply or divide the decimal by 2 the right number of times, and print what you're left holding.
The Plan 9 C library and the Go library both use variants of the approach above. On my laptop, the code above does 100,000 conversions per second, which is plenty for most uses, and the code is easy to understand.
Why are some converters more complicated than this? Because you can make them a little faster. On my laptop, glibc's sprintf(buf, "%.50e", M_PI) is about 15 times faster than an equivalent print using the code above, because the implementation of sprintf uses much more sophisticated mathematics to speed the conversion.
If you have a stomach for pages of equations, there are many interesting papers that discuss how to do this conversion and its inverse more quickly:
- William Clinger, “How to Read Floating Point Numbers Accurately”, PLDI 1990.
- Guy L. Steele Jr. and Jon L. White, “How to Print Floating Point Numbers Accurately”, PLDI 1990.
- David M. Gay, “Correctly Rounded Binary-Decimal and Decimal-Binary Conversions”, AT&T Bell Laboratories, 1990.
- Vern Paxson, “A Program for Testing IEEE Decimal-Binary Conversion”, May 1991.
- Robert Burger and R. Kent Dybvig, “Printing Floating-Point Numbers Quickly and Accurately”, SIGPLAN 1996.
- Florian Loitsch, “Printing Floating-Numbers Quickly and Accurately With Integers”, PLDI 2010.
Just remember: The conversion is easy. The optimizations are hard.
Code
<script src="https://ajax.googleapis.com/ajax/libs/jquery/1.6.1/jquery.min.js" type="text/javascript"></script> <script> function playground() { var code = encodeURIComponent($('').html(document.getElementById('code').innerHTML).text()) document.location = "http://golang.org/doc/play/#" + code } </script>The full program is available in this Gist or you can try it using the Go playground.
June 19, 2011
June 18, 2011
NineTimes - Inferno and Plan 9 News
9front propaganda
The Plan 9 community always was known to support intelligent jokes. 9front is taking this a bit further. Stanley Lieber (No, it's not him!) has created some artwork for 9front. Thanks to him!
May 19, 2011
OS Inferno
Inferno для Windows Mobile
May 18, 2011
research!rsc

Minimal Boolean Formulas
<style type="text/css"> p { line-height: 150%; } blockquote { text-align: left; } pre.alg { font-family: sans-serif; font-size: 100%; margin-left: 60px; } td, th { padding-left; 5px; padding-right: 5px; vertical-align: top; } #times td { text-align: right; } table { padding-top: 1em; padding-bottom: 1em; } #find td { text-align: center; } </style>
28. That's the minimum number of AND or OR operators you need in order to write any Boolean function of five variables. Alex Healy and I computed that in April 2010. Until then, I believe no one had ever known that little fact. This post describes how we computed it and how we almost got scooped by Knuth's Volume 4A which considers the problem for AND, OR, and XOR.
A Naive Brute Force Approach
Any Boolean function of two variables can be written with at most 3 AND or OR operators: the parity function on two variables X XOR Y is (X AND Y') OR (X' AND Y), where X' denotes “not X.” We can shorten the notation by writing AND and OR like multiplication and addition: X XOR Y = X*Y' + X'*Y.
For three variables, parity is also a hardest function, requiring 9 operators: X XOR Y XOR Z = (X*Z'+X'*Z+Y')*(X*Z+X'*Z'+Y).
For four variables, parity is still a hardest function, requiring 15 operators: W XOR X XOR Y XOR Z = (X*Z'+X'*Z+W'*Y+W*Y')*(X*Z+X'*Z'+W*Y+W'*Y').
The sequence so far prompts a few questions. Is parity always a hardest function? Does the minimum number of operators alternate between 2n−1 and 2n+1?
I computed these results in January 2001 after hearing the problem from Neil Sloane, who suggested it as a variant of a similar problem first studied by Claude Shannon.
The program I wrote to compute a(4) computes the minimum number of operators for every Boolean function of n variables in order to find the largest minimum over all functions. There are 24 = 16 settings of four variables, and each function can pick its own value for each setting, so there are 216 different functions. To make matters worse, you build new functions by taking pairs of old functions and joining them with AND or OR. 216 different functions means 216·216 = 232 pairs of functions.
The program I wrote was a mangling of the Floyd-Warshall all-pairs shortest paths algorithm. That algorithm is:
// Floyd-Warshall all pairs shortest path
func compute():
for each node i
for each node j
dist[i][j] = direct distance, or ∞
for each node k
for each node i
for each node j
d = dist[i][k] + dist[k][j]
if d < dist[i][j]
dist[i][j] = d
return
The algorithm begins with the distance table dist[i][j] set to an actual distance if i is connected to j and infinity otherwise. Then each round updates the table to account for paths going through the node k: if it's shorter to go from i to k to j, it saves that shorter distance in the table. The nodes are numbered from 0 to n, so the variables i, j, k are simply integers. Because there are only n nodes, we know we'll be done after the outer loop finishes.
The program I wrote to find minimum Boolean formula sizes is an adaptation, substituting formula sizes for distance.
// Algorithm 1
func compute()
for each function f
size[f] = ∞
for each single variable function f = v
size[f] = 0
loop
changed = false
for each function f
for each function g
d = size[f] + 1 + size[g]
if d < size[f OR g]
size[f OR g] = d
changed = true
if d < size[f AND g]
size[f AND g] = d
changed = true
if not changed
return
Algorithm 1 runs the same kind of iterative update loop as the Floyd-Warshall algorithm, but it isn't as obvious when you can stop, because you don't know the maximum formula size beforehand. So it runs until a round doesn't find any new functions to make, iterating until it finds a fixed point.
The pseudocode above glosses over some details, such as the fact that the per-function loops can iterate over a queue of functions known to have finite size, so that each loop omits the functions that aren't yet known. That's only a constant factor improvement, but it's a useful one.
Another important detail missing above is the representation of functions. The most convenient representation is a binary truth table. For example, if we are computing the complexity of two-variable functions, there are four possible inputs, which we can number as follows.
| X | Y | Value |
|---|---|---|
| false | false | 002 = 0 |
| false | true | 012 = 1 |
| true | false | 102 = 2 |
| true | true | 112 = 3 |
The functions are then the 4-bit numbers giving the value of the function for each input. For example, function 13 = 11012 is true for all inputs except X=false Y=true. Three-variable functions correspond to 3-bit inputs generating 8-bit truth tables, and so on.
This representation has two key advantages. The first is that the numbering is dense, so that you can implement a map keyed by function using a simple array. The second is that the operations “f AND g” and “f OR g” can be implemented using bitwise operators: the truth table for “f AND g” is the bitwise AND of the truth tables for f and g.
That program worked well enough in 2001 to compute the minimum number of operators necessary to write any 1-, 2-, 3-, and 4-variable Boolean function. Each round takes asymptotically O(22n·22n) = O(22n+1) time, and the number of rounds needed is O(the final answer). The answer for n=4 is 15, so the computation required on the order of 15·225 = 15·232 iterations of the innermost loop. That was plausible on the computer I was using at the time, but the answer for n=5, likely around 30, would need 30·264 iterations to compute, which seemed well out of reach. At the time, it seemed plausible that parity was always a hardest function and that the minimum size would continue to alternate between 2n−1 and 2n+1. It's a nice pattern.
Exploiting Symmetry
Five years later, though, Alex Healy and I got to talking about this sequence, and Alex shot down both conjectures using results from the theory of circuit complexity. (Theorists!) Neil Sloane added this note to the entry for the sequence in his Online Encyclopedia of Integer Sequences:
%E A056287 Russ Cox conjectures that X1 XOR ... XOR Xn is always a worst f and that a(5) = 33 and a(6) = 63. But (Jan 27 2006) Alex Healy points out that this conjecture is definitely false for large n. So what is a(5)?
Indeed. What is a(5)? No one knew, and it wasn't obvious how to find out.
In January 2010, Alex and I started looking into ways to speed up the computation for a(5). 30·264 is too many iterations but maybe we could find ways to cut that number.
In general, if we can identify a class of functions f whose members are guaranteed to have the same complexity, then we can save just one representative of the class as long as we recreate the entire class in the loop body. What used to be:
for each function f
for each function g
visit f AND g
visit f OR g
can be rewritten as
for each canonical function f
for each canonical function g
for each ff equivalent to f
for each gg equivalent to g
visit ff AND gg
visit ff OR gg
That doesn't look like an improvement: it's doing all the same work. But it can open the door to new optimizations depending on the equivalences chosen. For example, the functions “f” and “¬f” are guaranteed to have the same complexity, by DeMorgan's laws. If we keep just one of those two on the lists that “for each function” iterates over, we can unroll the inner two loops, producing:
for each canonical function f
for each canonical function g
visit f OR g
visit f AND g
visit ¬f OR g
visit ¬f AND g
visit f OR ¬g
visit f AND ¬g
visit ¬f OR ¬g
visit ¬f AND ¬g
That's still not an improvement, but it's no worse. Each of the two loops considers half as many functions but the inner iteration is four times longer. Now we can notice that half of tests aren't worth doing: “f AND g” is the negation of “¬f OR ¬g,” and so on, so only half of them are necessary.
Let's suppose that when choosing between “f” and “¬f”
we keep the one that is false when presented with all true inputs.
(This has the nice property that f ^ (int32(f) >> 31)
is the truth table for the canonical form of f.)
Then we can tell which combinations above will produce
canonical functions when f and g are already canonical:
for each canonical function f
for each canonical function g
visit f OR g
visit f AND g
visit ¬f AND g
visit f AND ¬g
That's a factor of two improvement over the original loop.
Another observation is that permuting the inputs to a function doesn't change its complexity: “f(V, W, X, Y, Z)” and “f(Z, Y, X, W, V)” will have the same minimum size. For complex functions, each of the 5! = 120 permutations will produce a different truth table. A factor of 120 reduction in storage is good but again we have the problem of expanding the class in the iteration. This time, there's a different trick for reducing the work in the innermost iteration. Since we only need to produce one member of the equivalence class, it doesn't make sense to permute the inputs to both f and g. Instead, permuting just the inputs to f while fixing g is guaranteed to hit at least one member of each class that permuting both f and g would. So we gain the factor of 120 twice in the loops and lose it once in the iteration, for a net savings of 120. (In some ways, this is the same trick we did with “f” vs “¬f.”)
A final observation is that negating any of the inputs to the function doesn't change its complexity, because X and X' have the same complexity. The same argument we used for permutations applies here, for another constant factor of 25 = 32.
The code stores a single function for each equivalence class and then recomputes the equivalent functions for f, but not g.
for each canonical function f
for each function ff equivalent to f
for each canonical function g
visit ff OR g
visit ff AND g
visit ¬ff AND g
visit ff AND ¬g
In all, we just got a savings of 2·120·32 = 7680, cutting the total number of iterations from 30·264 = 5×1020 to 7×1016. If you figure we can do around 109 iterations per second, that's still 800 days of CPU time.
The full algorithm at this point is:
// Algorithm 2
func compute():
for each function f
size[f] = ∞
for each single variable function f = v
size[f] = 0
loop
changed = false
for each canonical function f
for each function ff equivalent to f
for each canonical function g
d = size[ff] + 1 + size[g]
changed |= visit(d, ff OR g)
changed |= visit(d, ff AND g)
changed |= visit(d, ff AND ¬g)
changed |= visit(d, ¬ff AND g)
if not changed
return
func visit(d, fg):
if size[fg] != ∞
return false
record fg as canonical
for each function ffgg equivalent to fg
size[ffgg] = d
return true
The helper function “visit” must set the size not only of its argument fg but also all equivalent functions under permutation or inversion of the inputs, so that future tests will see that they have been computed.
Methodical Exploration
There's one final improvement we can make. The approach of looping until things stop changing considers each function pair multiple times as their sizes go down. Instead, we can consider functions in order of complexity, so that the main loop builds first all the functions of minimum complexity 1, then all the functions of minimum complexity 2, and so on. If we do that, we'll consider each function pair at most once. We can stop when all functions are accounted for.
Applying this idea to Algorithm 1 (before canonicalization) yields:
// Algorithm 3
func compute()
for each function f
size[f] = ∞
for each single variable function f = v
size[f] = 0
for k = 1 to ∞
for each function f
for each function g of size k − size(f) − 1
if size[f AND g] == ∞
size[f AND g] = k
nsize++
if size[f OR g] == ∞
size[f OR g] = k
nsize++
if nsize == 22n
return
Applying the idea to Algorithm 2 (after canonicalization) yields:
// Algorithm 4
func compute():
for each function f
size[f] = ∞
for each single variable function f = v
size[f] = 0
for k = 1 to ∞
for each canonical function f
for each function ff equivalent to f
for each canonical function g of size k − size(f) − 1
visit(k, ff OR g)
visit(k, ff AND g)
visit(k, ff AND ¬g)
visit(k, ¬ff AND g)
if nvisited == 22n
return
func visit(d, fg):
if size[fg] != ∞
return
record fg as canonical
for each function ffgg equivalent to fg
if size[ffgg] != ∞
size[ffgg] = d
nvisited += 2 // counts ffgg and ¬ffgg
return
The original loop in Algorithms 1 and 2 considered each pair f, g in every iteration of the loop after they were computed. The new loop in Algorithms 3 and 4 considers each pair f, g only once, when k = size(f) + size(g) + 1. This removes the leading factor of 30 (the number of times we expected the first loop to run) from our estimation of the run time. Now the expected number of iterations is around 264/7680 = 2.4×1015. If we can do 109 iterations per second, that's only 28 days of CPU time, which I can deliver if you can wait a month.
Our estimate does not include the fact that not all function pairs need to be considered. For example, if the maximum size is 30, then the functions of size 14 need never be paired against the functions of size 16, because any result would have size 14+1+16 = 31. So even 2.4×1015 is an overestimate, but it's in the right ballpark. (With hindsight I can report that only 1.7×1014 pairs need to be considered but also that our estimate of 109 iterations per second was optimistic. The actual calculation ran for 20 days, an average of about 108 iterations per second.)
Endgame: Directed Search
A month is still a long time to wait, and we can do better. Near the end (after k is bigger than, say, 22), we are exploring the fairly large space of function pairs in hopes of finding a fairly small number of remaining functions. At that point it makes sense to change from the bottom-up “bang things together and see what we make” to the top-down “try to make this one of these specific functions.” That is, the core of the current search is:
for each canonical function f
for each function ff equivalent to f
for each canonical function g of size k − size(f) − 1
visit(k, ff OR g)
visit(k, ff AND g)
visit(k, ff AND ¬g)
visit(k, ¬ff AND g)
We can change it to:
for each missing function fg
for each canonical function g
for all possible f such that one of these holds
* fg = f OR g
* fg = f AND g
* fg = ¬f AND g
* fg = f AND ¬g
if size[f] == k − size(g) − 1
visit(k, fg)
next fg
By the time we're at the end, exploring all the possible f to make the missing functions—a directed search—is much less work than the brute force of exploring all combinations.
As an example, suppose we are looking for f such that fg = f OR g. The equation is only possible to satisfy if fg OR g == fg. That is, if g has any extraneous 1 bits, no f will work, so we can move on. Otherwise, the remaining condition is that f AND ¬g == fg AND ¬g. That is, for the bit positions where g is 0, f must match fg. The other bits of f (the bits where g has 1s) can take any value. We can enumerate the possible f values by recursively trying all possible values for the “don't care” bits.
func find(x, any, xsize):
if size(x) == xsize
return x
while any != 0
bit = any AND −any // rightmost 1 bit in any
any = any AND ¬bit
if f = find(x OR bit, any, xsize) succeeds
return f
return failure
It doesn't matter which 1 bit we choose for the recursion, but finding the rightmost 1 bit is cheap: it is isolated by the (admittedly surprising) expression “any AND −any.”
Given find, the loop above can try these four cases:
| Formula | Condition | Base x | “Any” bits |
|---|---|---|---|
| fg = f OR g | fg OR g == fg | fg AND ¬g | g |
| fg = f OR ¬g | fg OR ¬g == fg | fg AND g | ¬g |
| ¬fg = f OR g | ¬fg OR g == fg | ¬fg AND ¬g | g |
| ¬fg = f OR ¬g | ¬fg OR ¬g == ¬fg | ¬fg AND g | ¬g |
Rewriting the Boolean expressions to use only the four OR forms means that we only need to write the “adding bits” version of find.
The final algorithm is:
// Algorithm 5
func compute():
for each function f
size[f] = ∞
for each single variable function f = v
size[f] = 0
// Generate functions.
for k = 1 to max_generate
for each canonical function f
for each function ff equivalent to f
for each canonical function g of size k − size(f) − 1
visit(k, ff OR g)
visit(k, ff AND g)
visit(k, ff AND ¬g)
visit(k, ¬ff AND g)
// Search for functions.
for k = max_generate+1 to ∞
for each missing function fg
for each canonical function g
fsize = k − size(g) − 1
if fg OR g == fg
if f = find(fg AND ¬g, g, fsize) succeeds
visit(k, fg)
next fg
if fg OR ¬g == fg
if f = find(fg AND g, ¬g, fsize) succeeds
visit(k, fg)
next fg
if ¬fg OR g == ¬fg
if f = find(¬fg AND ¬g, g, fsize) succeeds
visit(k, fg)
next fg
if ¬fg OR ¬g == ¬fg
if f = find(¬fg AND g, ¬g, fsize) succeeds
visit(k, fg)
next fg
if nvisited == 22n
return
func visit(d, fg):
if size[fg] != ∞
return
record fg as canonical
for each function ffgg equivalent to fg
if size[ffgg] != ∞
size[ffgg] = d
nvisited += 2 // counts ffgg and ¬ffgg
return
func find(x, any, xsize):
if size(x) == xsize
return x
while any != 0
bit = any AND −any // rightmost 1 bit in any
any = any AND ¬bit
if f = find(x OR bit, any, xsize) succeeds
return f
return failure
To get a sense of the speedup here, and to check my work, I ran the program using both algorithms on a 2.53 GHz Intel Core 2 Duo E7200.
| ————— # of Functions ————— | ———— Time ———— | ||||
|---|---|---|---|---|---|
| Size | Canonical | All | All, Cumulative | Generate | Search |
| 0 | 1 | 10 | 10 | ||
| 1 | 2 | 82 | 92 | < 0.1 seconds | 3.4 minutes |
| 2 | 2 | 640 | 732 | < 0.1 seconds | 7.2 minutes |
| 3 | 7 | 4420 | 5152 | < 0.1 seconds | 12.3 minutes |
| 4 | 19 | 25276 | 29696 | < 0.1 seconds | 30.1 minutes |
| 5 | 44 | 117440 | 147136 | < 0.1 seconds | 1.3 hours |
| 6 | 142 | 515040 | 662176 | < 0.1 seconds | 3.5 hours |
| 7 | 436 | 1999608 | 2661784 | 0.2 seconds | 11.6 hours |
| 8 | 1209 | 6598400 | 9260184 | 0.6 seconds | 1.7 days |
| 9 | 3307 | 19577332 | 28837516 | 1.7 seconds | 4.9 days |
| 10 | 7741 | 50822560 | 79660076 | 4.6 seconds | [ 10 days ? ] |
| 11 | 17257 | 114619264 | 194279340 | 10.8 seconds | [ 20 days ? ] |
| 12 | 31851 | 221301008 | 415580348 | 21.7 seconds | [ 50 days ? ] |
| 13 | 53901 | 374704776 | 790285124 | 38.5 seconds | [ 80 days ? ] |
| 14 | 75248 | 533594528 | 1323879652 | 58.7 seconds | [ 100 days ? ] |
| 15 | 94572 | 667653642 | 1991533294 | 1.5 minutes | [ 120 days ? ] |
| 16 | 98237 | 697228760 | 2688762054 | 2.1 minutes | [ 120 days ? ] |
| 17 | 89342 | 628589440 | 3317351494 | 4.1 minutes | [ 90 days ? ] |
| 18 | 66951 | 468552896 | 3785904390 | 9.1 minutes | [ 50 days ? ] |
| 19 | 41664 | 287647616 | 4073552006 | 23.4 minutes | [ 30 days ? ] |
| 20 | 21481 | 144079832 | 4217631838 | 57.0 minutes | [ 10 days ? ] |
| 21 | 8680 | 55538224 | 4273170062 | 2.4 hours | 2.5 days |
| 22 | 2730 | 16099568 | 4289269630 | 5.2 hours | 11.7 hours |
| 23 | 937 | 4428800 | 4293698430 | 11.2 hours | 2.2 hours |
| 24 | 228 | 959328 | 4294657758 | 22.0 hours | 33.2 minutes |
| 25 | 103 | 283200 | 4294940958 | 1.7 days | 4.0 minutes |
| 26 | 21 | 22224 | 4294963182 | 2.9 days | 42 seconds |
| 27 | 10 | 3602 | 4294966784 | 4.7 days | 2.4 seconds |
| 28 | 3 | 512 | 4294967296 | [ 7 days ? ] | 0.1 seconds |
The bracketed times are estimates based on the work involved: I did not wait that long for the intermediate search steps. The search algorithm is quite a bit worse than generate until there are very few functions left to find. However, it comes in handy just when it is most useful: when the generate algorithm has slowed to a crawl. If we run generate through formulas of size 22 and then switch to search for 23 onward, we can run the whole computation in just over half a day of CPU time.
The computation of a(5) identified the sizes of all 616,126 canonical Boolean functions of 5 inputs. In contrast, there are just over 200 trillion canonical Boolean functions of 6 inputs. Determining a(6) is unlikely to happen by brute force computation, no matter what clever tricks we use.
Adding XOR
We've assumed the use of just AND and OR as our basis for the Boolean formulas. If we also allow XOR, functions can be written using many fewer operators. In particular, a hardest function for the 1-, 2-, 3-, and 4-input cases—parity—is now trivial. Knuth examines the complexity of 5-input Boolean functions using AND, OR, and XOR in detail in The Art of Computer Programming, Volume 4A. Section 7.1.2's Algorithm L is the same as our Algorithm 3 above, given for computing 4-input functions. Knuth mentions that to adapt it for 5-input functions one must treat only canonical functions and gives results for 5-input functions with XOR allowed. So another way to check our work is to add XOR to our Algorithm 4 and check that our results match Knuth's.
Because the minimum formula sizes are smaller (at most 12), the computation of sizes with XOR is much faster than before:
| ————— # of Functions ————— | ||||||||
|---|---|---|---|---|---|---|---|---|
| Size | Canonical | All | All, Cumulative | Time | ||||
| 0 | 1 | 10 | 10 | |||||
| 1 | 3 | 102 | 112 | < 0.1 seconds | ||||
| 2 | 5 | 1140 | 1252 | < 0.1 seconds | ||||
| 3 | 20 | 11570 | 12822 | < 0.1 seconds | ||||
| 4 | 93 | 109826 | 122648 | < 0.1 seconds | ||||
| 5 | 366 | 936440 | 1059088 | 0.1 seconds | ||||
| 6 | 1730 | 7236880 | 8295968 | 0.7 seconds | ||||
| 7 | 8782 | 47739088 | 56035056 | 4.5 seconds | ||||
| 8 | 40297 | 250674320 | 306709376 | 24.0 seconds | ||||
| 9 | 141422 | 955812256 | 1262521632 | 95.5 seconds | ||||
| 10 | 273277 | 1945383936 | 3207905568 | 200.7 seconds | ||||
| 11 | 145707 | 1055912608 | 4263818176 | 121.2 seconds | ||||
| 12 | 4423 | 31149120 | 4294967296 | 65.0 seconds | ||||
Knuth does not discuss anything like Algorithm 5,
because the search for specific functions does not apply to
the AND, OR, and XOR basis. XOR is a non-monotone
function (it can both turn bits on and turn bits off), so
there is no test like our “if fg OR g == fg”
and no small set of “don't care” bits to trim the search for f.
The search for an appropriate f in the XOR case would have
to try all f of the right size, which is exactly what Algorithm 4 already does.
Volume 4A also considers the problem of building minimal circuits, which are like formulas but can use common subexpressions additional times for free, and the problem of building the shallowest possible circuits. See Section 7.1.2 for all the details.
Code and Web Site
The web site boolean-oracle.swtch.com lets you type in a Boolean expression and gives back the minimal formula for it. It uses tables generated while running Algorithm 5; those tables and the programs described in this post are also available on the site.
Postscript: Generating All Permutations and Inversions
The algorithms given above depend crucially on the step
“for each function ff equivalent to f,”
which generates all the ff obtained by permuting or inverting inputs to f,
but I did not explain how to do that.
We already saw that we can manipulate the binary truth table representation
directly to turn f into ¬f and to compute
combinations of functions.
We can also manipulate the binary representation directly to
invert a specific input or swap a pair of adjacent inputs.
Using those operations we can cycle through all the equivalent functions.
To invert a specific input, let's consider the structure of the truth table. The index of a bit in the truth table encodes the inputs for that entry. For example, the low bit of the index gives the value of the first input. So the even-numbered bits—at indices 0, 2, 4, 6, ...—correspond to the first input being false, while the odd-numbered bits—at indices 1, 3, 5, 7, ...—correspond to the first input being true. Changing just that bit in the index corresponds to changing the single variable, so indices 0, 1 differ only in the value of the first input, as do 2, 3, and 4, 5, and 6, 7, and so on. Given the truth table for f(V, W, X, Y, Z) we can compute the truth table for f(¬V, W, X, Y, Z) by swapping adjacent bit pairs in the original truth table. Even better, we can do all the swaps in parallel using a bitwise operation. To invert a different input, we swap larger runs of bits.
| Function | Truth Table (f = f(V, W, X, Y, Z))
| |
|---|---|---|
| f(¬V, W, X, Y, Z) | (f&0x55555555)<< 1 | (f>> 1)&0x55555555
| |
| f(V, ¬W, X, Y, Z) | (f&0x33333333)<< 2 | (f>> 2)&0x33333333
| |
| f(V, W, ¬X, Y, Z) | (f&0x0f0f0f0f)<< 4 | (f>> 4)&0x0f0f0f0f
| |
| f(V, W, X, ¬Y, Z) | (f&0x00ff00ff)<< 8 | (f>> 8)&0x00ff00ff
| |
| f(V, W, X, Y, ¬Z) | (f&0x0000ffff)<<16 | (f>>16)&0x0000ffff
|
Being able to invert a specific input lets us consider all possible inversions by building them up one at a time. The Gray code lets us enumerate all possible 5-bit input codes while changing only 1 bit at a time as we move from one input to the next:
12, 13, 15, 14, 10, 11, 9, 8,
24, 25, 27, 26, 30, 31, 29, 28,
20, 21, 23, 22, 18, 19, 17, 16
This minimizes the number of inversions we need: to consider all 32 cases, we only need 31 inversion operations. In contrast, visiting the 5-bit input codes in the usual binary order 0, 1, 2, 3, 4, ... would often need to change multiple bits, like when changing from 3 to 4.
To swap a pair of adjacent inputs, we can again take advantage of the truth table. For a pair of inputs, there are four cases: 00, 01, 10, and 11. We can leave the 00 and 11 cases alone, because they are invariant under swapping, and concentrate on swapping the 01 and 10 bits. The first two inputs change most often in the truth table: each run of 4 bits corresponds to those four cases. In each run, we want to leave the first and fourth alone and swap the second and third. For later inputs, the four cases consist of sections of bits instead of single bits.
| Function | Truth Table (f = f(V, W, X, Y, Z))
| |
|---|---|---|
| f(W, V, X, Y, Z) | f&0x99999999 | (f&0x22222222)<<1 | (f>>1)&0x22222222
| |
| f(V, X, W, Y, Z) | f&0xc3c3c3c3 | (f&0x0c0c0c0c)<<1 | (f>>1)&0x0c0c0c0c
| |
| f(V, W, Y, X, Z) | f&0xf00ff00f | (f&0x00f000f0)<<1 | (f>>1)&0x00f000f0
| |
| f(V, W, X, Z, Y) | f&0xff0000ff | (f&0x0000ff00)<<8 | (f>>8)&0x0000ff00
|
Being able to swap a pair of adjacent inputs lets us consider all possible permutations by building them up one at a time. Again it is convenient to have a way to visit all permutations by applying only one swap at a time. Here Volume 4A comes to the rescue. Section 7.2.1.2 is titled “Generating All Permutations,” and Knuth delivers many algorithms to do just that. The most convenient for our purposes is Algorithm P, which generates a sequence that considers all permutations exactly once with only a single swap of adjacent inputs between steps. Knuth calls it Algorithm P because it corresponds to the “Plain changes” algorithm used by bell ringers in 17th century England to ring a set of bells in all possible permutations. The algorithm is described in a manuscript written around 1653!
We can examine all possible permutations and inversions by nesting a loop over all permutations inside a loop over all inversions, and in fact that's what my program does. Knuth does one better, though: his Exercise 7.2.1.2-20 suggests that it is possible to build up all the possibilities using only adjacent swaps and inversion of the first input. Negating arbitrary inputs is not hard, though, and still does minimal work, so the code sticks with Gray codes and Plain changes.
May 15, 2011
May 10, 2011
OS Inferno
Plan9front - очередной форк plan9
Это не было бы столь интересно, если бы автор не успевал "строчить" по 10-20 коммитов ежедневно, а список изменений не был бы таким занимательным:
* 9load заменен на более развитый 9boot.
* Файловая система fossil заменена на cwfs.
* Язык программирования и среда исполнения языка Go.
* Новый файловый сервер kbdfs.
* Возможность установки с USB CD-ROM, USB HDD и USB FLASH.
* SMB-сервер cifsd в комплекте.
* Python и Mercurial.
* Эмулятор tty.
* Эмулятор /dev/realmode realemu, позволяющий активировать графический режим на ранее не поддерживаемых видео-картах.
* Драйвера для следующих устройств: сетевая карта Broadcom BCM57xx, SATA-контроллеры Intel 82801FBM SATA, ntel 82801HB/HR/HH/HO SATA IDE, ntel 82801HBM SATA (ICH8-M), видео-карты AMD Geode LX, планшетов Wacom WACF004 и WACF008.